3

I've read a lot of questions about rings but I still don't know why they are useful/ I'm sure they are, but I don't know why. Are their properties somehow used in proofs or as foundations for theorems? And what exactly do mathematicians study when they research rings? Can you give some examples?

GuPe
  • 7,318
  • 2
    Wikipedia has a good start: "Theorems from arithmetic are extended to non-numerical objects like polynomials, series, matrices and functions" – White Shirt Jun 29 '15 at 18:32
  • Rings are useful in the same way that groups are useful. It allows us to work in a system which has two "operations" which we often call "addition" and "multiplication" (though the "addition" and "multiplication" might have nothing to do with the addition and multiplication that we are used to) such that these operations satisfy some "nice" properties. – JMoravitz Jun 29 '15 at 18:33
  • 1
    Mathematics always has the goal to solve many problems simultanesly, so ring a an abstraction and one can proof result for all rings, which are useful for numbers, polynomials etc. – epsilon Jun 29 '15 at 18:56
  • See http://math.stackexchange.com/a/83987/589. – lhf Jun 29 '15 at 19:52
  • If $X$ is an Abelian group (aka a $\mathbb{Z}$-module), then $\mathrm{End}(X)$ is a ring (aka a $\mathbb{Z}$-algebra.) More generally, given a commutative ring $R$, we have that if $X$ is an $R$-module, then $\mathrm{End}(X)$ is an $R$-algebra. For example, $\mathbb{R}$-algebras of real-valued square matrices can be understood as arising in this fashion. – goblin GONE Jun 29 '15 at 20:07
  • Questions like this deserve a wide variety of answers. That will not occur if you quickly accept the first answer; e.g. many experts do not even bother to read questions that already have an accepted answer. Generally it is a good idea to wait a few days before accepting. – Bill Dubuque Jun 29 '15 at 20:20

1 Answers1

9

Although I am not much of an Algebraic Geometry person, but it is a very important application of commutative ring theory. Just to give you a flavor, here is a brief idea.

Consider the ring $\Bbb{C}$. Now we do like to study surfaces/curves (that is an application, right!) , and we define them by equations in rings $R=\Bbb{C}[x_1,x_2,\dots , x_n]$.

Now suppose $p(x)\in R$ is a polynomial, and we need to find zeroes of this polynomial (for same reasons we find zeros of quadratics in single variable, they help us study surfaces and many things), then it is not as straightforward as a quadratic\cubic equation in $\Bbb{C}[x]$.
We need the locus $X=V(p(x))=\{t=(a_1,a_2,\dots , a_n): p(t)=0\}\subseteq \Bbb{C^n}$

Now consider the residue ring $A=\Bbb{C}[x_1,x_2,\dots , x_n]/(p(x))$. Now a proposition in algebraic geometry (in beginning of it) says Maximal ideals of $A$ are in one-one correspondence with points $P\in X$. So studying maximal ideals of these rings gives us solution of those multivariable polynomials.

For Example, Consider the Curve $x^3-y^2 \in \Bbb{C}[x,y]$.

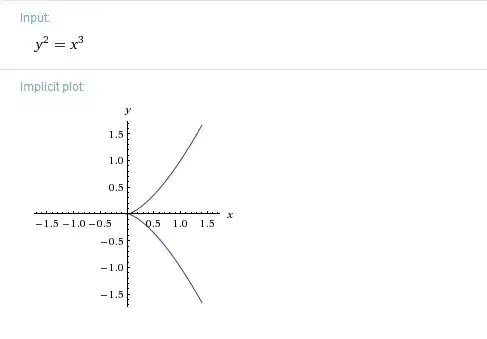
enter image description here

Now to find set of complex 2-tuples such that they satisfy $x^3-y^2=0$ (i.e. solutions), we can correspond them with maximal ideals of the ring $A=\Bbb{C}[x,y]/(x^3-y^2)$ , and $A$ can be realized as the same ring $A'=\Bbb{C}[x][\sqrt{x^3}]$ and by Hilbert Nullstellensatz, maximal ideals of $A'$ are of the form $(x-a,y-b)$ where $b=\pm\sqrt{a^3}$, $a,b\in \Bbb{C}$ .

Also clearly $A'=\Bbb{C}[x][\sqrt{x^3}] \subset \Bbb{C}[\sqrt{x}]$, then letting $t=\sqrt{x}$, we see $A' \subset \Bbb{C}[t]$, where $\Bbb{C}[t]$ is a PID and all its ideals are maximals, must be useful, though I am not sure how exactly.

Similarly local rings (rings with a unique maximal ideal) are of utmost importance in algebraic geometry, and we can get a local ring from any ring via Localization process and then study curves/surfaces over them is useful etc.

Study of ideals of rings, finding all the prime ideals and maximal ideals of various rings helps us in many branches of maths, esp. in Algebraic geometry.

It is just one of the many important things, rings offer us. Just do not forget all fields are rings, and fields are important to us as from the very beginning we liked working with real and complex number, which both are fields and therefore rings.

We use Galois theory to prove every quintic is unsolvable by radicals etc. Rings play important part in algebraic number theory and helped proving as big and important conjectures as Fermat's Last theorem.

Bhaskar Vashishth
  • 11,279
  • 3
    (+1) If someone had explained some Algebraic Geometry to me when I was learning about rings, I might have actually cared about them... – Chappers Jun 29 '15 at 19:31
  • Ring is essentially a kingdom of polynomials. – Piquito Jun 29 '15 at 19:59
  • I understand this because I know what you are saying, but the exposition is a bit confused. For example, could you clarify the sentence: "Now we do like to study surfaces [...] and we define them by curves in rings"? – A.P. Jun 29 '15 at 20:48
  • @A.P. I tried editing, please check, and if there is some mistake, lemme know or feel free to edit I have only introductory knowledge of algebraic geometry which I learned from commutative algebra course. – Bhaskar Vashishth Jun 29 '15 at 21:59
  • 1
    Nice of you to add an example. It still isn't clear from this why or how the point of view of algebraic geometry can be useful, though. By the way, The inclusion $A' \subset \Bbb{C}[t]$ induces (on spectra) a nice morphism from the affine line to the cusp: think of projecting the $y$-axis onto the cusp. – A.P. Jun 30 '15 at 08:29