I have a camera looking at a computer monitor from varying angles. Since the camera is a grid of pixels, I can define the bounds of the monitor in the camera image as:
I hope that makes sense. What I want to do is come up with an algorithm to translate points within this shape to this:
I have points within the same domain as ABCD, as determined from the camera, but I need to draw these points in the domain of the monitor's resolution.
Does that makes sense? Any ideas?
In general there is no affine transformation that maps an arbitrary quadrangle onto a rectangle. But there is (exactly one) projective transformation $T$ that maps a given quadrangle $(A, B, C, D)$ in the projective plane onto a given quadrangle $(A', B', C' D')$ in the same or another projective plane. This $T$ is ${\it collinear}$, i.e., it maps lines to lines. To do the calculations you have to introduce homogeneous coordinates $(x,y,z)$ such that $D=(0,0,1)$, $C=(1,0,1)$, $A=(0,1,1)$, $B=(1,1,1)$ and similarly for $A'$, $B'$, $C'$, $D'$. With respect to these coordinates the map $T$ is linear and its matrix is the identity matrix.
The best solution I've found so far on a forum lost in the sea of forums is to decompose your problem like this :
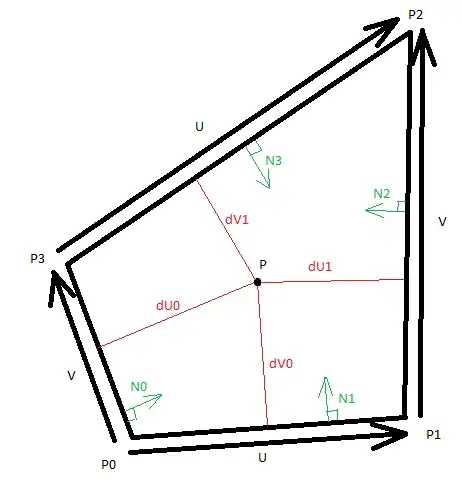
Here, U and V represent coordinates within the quadrilateral (scaled between 0 and 1).
From $P0$, $P1$, $P2$ & $P3$ we can easily compute the normalized normal vectors $N0$, $N1$, $N2$ & $N3$. Then, it's easy to see that : $$u = \frac{dU0}{dU0 + dU1} = \frac{(P-P0) \cdot N0}{(P-P0).N0 + (P-P2) \cdot N2} \\ v = \frac{dV0}{dV0 + dV1} = \frac{(P-P0) \cdot N1}{(P-P0).N1 + (P-P3) \cdot N3}.$$
This parametrization works like a charm and is really easy to compute within a shader for example. What's tricky is the reverse: finding $P(x,y)$ from $(u,v)$ so here is the result:
$$x = \frac{vKH \cdot uFC - vLI \cdot uEB}{vJG \cdot uEB - vKH \cdot uDA}, \\ y = \frac{vLI \cdot uDA - uFC \cdot vJG}{vJG \cdot uEB - vKH \cdot uDA},$$
where: $$uDA = u \cdot (D-A), \quad uEB = u \cdot (E-B), \quad uFC = u \cdot (F-C), \\ vJG = v \cdot (J-G), \quad vKH = v \cdot (K-H), \quad vJG = v \cdot (J-G),$$
and finally: $$A = N0_x, \qquad \qquad B = N0_y, \quad C = -P0 \cdot N0, \qquad \\ D = N0_x + N2_x, \quad E = N0_y + N2_y, \quad F = -P0 \cdot N0 - P2 \cdot N2, \\ G = N1_x, \qquad \qquad H = N1_y, \quad I = -P0 \cdot N1, \qquad \\ J = N1_x + N3_x, \quad K = N1_y + N3_y, \quad L = -P0 \cdot N1 - P2 \cdot N3.$$
I've been using this successfully for shadow mapping of a deformed camera frustum mapped into a regular square texture and I can assure you it's working great! :D
Take a look on Gernot Hoffmann's tutorial on image rectification. There are also the special cases (rectangle to quadrilateral) explained.
Another page that helped me discusses 2D perspective transformation (i.e. planar homography).
For a deep understanding of the topic and more numerically stable algorithms, I can only recommend Hartley & Zisserman: Multi-View Geometry in Computer Vision.
Here is a solution implemented in VBA, a General Algebraic solution, more general than the augmented 2D affine transformation formulation on Wikipedia.
Function Quad_to_Logical_Cell(Qx() As Double, Qy() As Double, x As Double, y As Double) As Variant
'WJW 7-13-15
'This function performs a coordinate transform from X,Y space to the normalized L,M.
'
'If a point {is within {0,1} on both axes, it is within the transformed unit square.
'Qx,Qy vectors contain the 4 coordinates of the corners - x and y values, respectively, ordered as indicated below:
'
'The unit cell L(l,m) corresponding to Q(x,y) is oriented as:
'L0(x=0,y=0),L1(0,1), L2(1,1), L3(1,0). The order matters.
'The following represent an algebraic solution to the system:
'l=a1 + b1x + c1y + d1xy
'm=a2 + b2x + c2y + d2xy
Dim L_Out() As Double
ReDim L_Out(2)
ax = (x - Qx(0)) + (Qx(1) - Qx(0)) * (y - Qy(0)) / (Qy(0) - Qy(1))
a3x = (Qx(3) - Qx(0)) + (Qx(1) - Qx(0)) * (Qy(3) - Qy(0)) / (Qy(0) - Qy(1))
a2x = (Qx(2) - Qx(0)) + (Qx(1) - Qx(0)) * (Qy(2) - Qy(0)) / (Qy(0) - Qy(1))
ay = (y - Qy(0)) + (Qy(3) - Qy(0)) * (x - Qx(0)) / (Qx(0) - Qx(3))
a1y = (Qy(1) - Qy(0)) + (Qy(3) - Qy(0)) * (Qx(1) - Qx(0)) / (Qx(0) - Qx(3))
a2y = (Qy(2) - Qy(0)) + (Qy(3) - Qy(0)) * (Qx(2) - Qx(0)) / (Qx(0) - Qx(3))
bx = x * y - Qx(0) * Qy(0) + (Qx(1) * Qy(1) - Qx(0) * Qy(0)) * (y - Qy(0)) / (Qy(0) - Qy(1))
b3x = Qx(3) * Qy(3) - Qx(0) * Qy(0) + (Qx(1) * Qy(1) - Qx(0) * Qy(0)) * (Qy(3) - Qy(0)) / (Qy(0) - Qy(1))
b2x = Qx(2) * Qy(2) - Qx(0) * Qy(0) + (Qx(1) * Qy(1) - Qx(0) * Qy(0)) * (Qy(2) - Qy(0)) / (Qy(0) - Qy(1))
by = x * y - Qx(0) * Qy(0) + (Qx(3) * Qy(3) - Qx(0) * Qy(0)) * (x - Qx(0)) / (Qx(0) - Qx(3))
b1y = Qx(1) * Qy(1) - Qx(0) * Qy(0) + (Qx(3) * Qy(3) - Qx(0) * Qy(0)) * (Qx(1) - Qx(0)) / (Qx(0) - Qx(3))
b2y = Qx(2) * Qy(2) - Qx(0) * Qy(0) + (Qx(3) * Qy(3) - Qx(0) * Qy(0)) * (Qx(2) - Qx(0)) / (Qx(0) - Qx(3))
'Dependent on the way your data is formatted, you may have to swap x and y to get the order right.
'L=L(0) is the x coordinate here (row)
'M=L(1) is the y coordinate here (colum)
L_Out(0) = (ax / a3x) + (1 - a2x / a3x) * (bx - b3x * ax / a3x) / (b2x - b3x * a2x / a3x)
L_Out(1) = (ay / a1y) + (1 - a2y / a1y) * (by - b1y * ay / a1y) / (b2y - b1y * a2y / a1y)
Quad_to_Logical_Cell = L_Out
End Function
Try this solution, it worked for me.
I've been wrestling with a very similar problem in order to determine gradients in an irregular quad grid and needing to map points within arbitrary quadrilaterals to a unit square. In addition, I require the inverse mapping of the x and y axis at the mapped normalized coordinate location back into the quad so I can determine the orientation of the quad grid at that point. i.e. if [x',y'] are the transformed coordinates, I need to be able to do an inverse transform on [0,y'],[1,y'] and [x',0],[x',1]. Here is what I've come up with:
You can divide the quad into two tris, and use affine maps on these individually. This is not difficult. This will create a noticable effect at the division between the two tris, however.
If you want a smooth mapping from a quad to a square (or rectangle), you need to use a non-affine transform such as a projective transform. There are other transforms other than projective that will also work, and also be colinear (preserve straight lines).
If [x1,y1],[x2,y2],[x3,y3],[x4,y4] are the four points in the quad, then the 4x4 matrix B in the the following will yield a mapping into the square (on the RHS) that seems to work and may be easier to compute than the proper 3x3 projective matrix.
% [x1 y1 x1*y1 1] [0 0 0 1]
% [x2 y2 x2*y2 1] X B = [1 0 0 1]
% [x3 y3 x3*y3 1] [0 1 0 1]
% [x4 y4 x4*y4 1] [1 1 1 1]
The question I have is that if one does this, and then wants to use the inverse of B to do the inverse transform, how do you calculate the third elements of the location vectors for the orthogonal coordinates. (They are no longer x*y.)
NOTE: If you want to map into any other (arbitrary) quadrilateral (such as a rectangle), then just replace the RHS of what I have above with the new coordinates.
% [x1 y1 x1*y1 1] [x1' y1' x1'*y1' 1]
% [x2 y2 x2*y2 1] X B = [x2' y2' x2'*y2' 1]
% [x3 y3 x3*y3 1] [x3' y3' x3'*y3' 1]
% [x4 y4 x4*y4 1] [x4' y4' x4'*y4' 1]
You could approach this by using an isoparametric mapping. Say the quadrilateral object is said to be in a $x_{1}-y_1$ coordinate frame, while the rectangle is in a new $x_{2}-y_{2}$ frame. What you can do is find $x_{1}=x_{1}(x_{2},y_{2})$ and $y_{1}=y_{1}(x_{2},y_{2})$ using an interpolation-based mapping.
Say we define each vertex as a 2D vector $\vec{P}_{i}$, we can end up with the following mapping to find an a given $\vec{P}$ as a function of $x_{2}$ and $y_{2}$:
$$ \vec{P}(x_{2},y_{2}) = \sum_{i=1}^{4}\vec{P}_{i}h_{i}(x_{2},y_{2})$$
Now, assume point A, $\vec{P}_{1}$, corresponds with $(0,0)$ location, point B, $\vec{P}_{2}$, corresponds with $(width,0)=(w,0)$, etc. With that, we can arrive at the following expressions for $h_{i}$:
$$h_{1}(x_{2},y_2) = \frac{(x_{2}-w)(y_{2}-h)}{wh}$$
$$h_{2}(x_{2},y_2) = \frac{x_{2}(h-y_{2})}{wh}$$
$$h_{3}(x_{2},y_2) = \frac{x_{2}y_{2}}{wh}$$
$$h_{4}(x_{2},y_2) = \frac{(w-x_{2})y_{2}}{wh}$$
Using all this information, you could loop through the rectangle to find the $\vec{P}$ coordinate in the original image that each $(x_2,y_2)$ pixel is associated with, then get the pixel information and drop it into the $(x_2,y_2)$ pixel. As a note, the $h_i$ expressions were found via Lagrangian interpolation procedures.
Building off of @Patapom's answer, the goal is to find the $\mathbf{p}$ in image space corresponding to an arbitrary u,v. Starting from the transform:
$u = \frac{(\mathbf{p}-\mathbf{p_{0}}) \cdot \mathbf{n}_{0}}{(\mathbf{p}-\mathbf{p_{0}}).\mathbf{n}_{0} + (\mathbf{p}-\mathbf{p_{2}}) \cdot \mathbf{n}_{2}} \\ v = \frac{(\mathbf{p}-\mathbf{p_{0}}) \cdot \mathbf{n}_{1}}{(\mathbf{p}-\mathbf{p_{0}}).\mathbf{n}_{1} + (\mathbf{p}-\mathbf{p_{3}}) \cdot \mathbf{n}_{3}}.$
We can isolate $\mathbf{p}$, and rewrite the equality as $A\mathbf{p}=\mathbf{b}$, where:
$ A \equiv \begin{bmatrix} u \mathbf{n}_{2}^{\top}-(1-u) \mathbf{n}_{0}^{\top} \\ v \mathbf{n}_{3}^{\top}-(1-v) \mathbf{n}_{1}^{\top} \end{bmatrix} $
$ b \equiv \begin{bmatrix} u \mathbf{p}^{\top}_{2}\mathbf{n}_{2} - (1-u)\mathbf{p}^{\top}_{0}\mathbf{n}_{0} \\ v \mathbf{p}^{\top}_{3}\mathbf{n}_{3} - (1-v)\mathbf{p}^{\top}_{0}\mathbf{n}_{1} \end{bmatrix} $
Since A is a 2x2 matrix it can analytically inverted to solve for $\mathbf{p}$. Here's an example python routine:
def map_uv_to_xy(u, v, P, N):
nu = 1 - u
nv = 1 - v
A_11 = u*N[2][0]-nu*N[0][0]
A_12 = u*N[2][1]-nu*N[0][1]
A_21 = v*N[3][0]-nv*N[1][0]
A_22 = v*N[3][1]-nv*N[1][1]
b_0 = u*(P[2][0]*N[2][0] + P[2][1]*N[2][1])-nu*(P[0][0]*N[0][0] + P[0][1]*N[0][1])
b_1 = v*(P[3][0]*N[3][0] + P[3][1]*N[3][1])-nv*(P[0][0]*N[1][0] + P[0][1]*N[1][1])
x = b_0* A_22 + b_1*-A_12
y = b_0*-A_21 + b_1* A_11
det_A = A_11*A_22 - A_12*A_21
return x/det_A, y/det_A
I found this explanation easy to understand if you are familiar with basic linear algebra: http://faculty.salina.k-state.edu/tim/mVision/ImageFormation/homography.html
The basic idea is that you have 2x4 matrices $\mathbf{P}$ (coordinates of the four corners in the image you have) and $\mathbf{Q}$ (coordinates of the four corners in the projection you want, and you are trying to estimate $\mathbf{H}$ where $\mathbf{Q}=\mathbf{H}\mathbf{P}$, using the pseudoinverse:
$$\mathbf{H} = \mathbf{Q}\mathbf{P}^T(\mathbf{P}\mathbf{P}^T)^{-1}$$
or use a least-square estimator (like numpy.linalg.lstsq in Python) to solve $\mathbf{Q}=\mathbf{H}\mathbf{P}$ for $\mathbf{H}$.
HINT
$A,B,C,D$ are not in the same plane.
A very approximate rectangular projection ratio ... by area projections with extended boundary length), may be obtained considering boundary vector lenghts.
$$\frac{\frac12(|u \times v|+|w \times a|)}{(|u|+|v|+|w|+|a|)^2}$$
The rectangle can be now re-sized.
