If $\arctan(x)+\arctan(y)+\arctan(z)=\pi/2$ how to show that $xy+yz+zx=1$?

Question

If $\arctan(x)+\arctan(y)+\arctan(z)=\pi/2$ how to show that $xy+yz+zx=1$ ?

Answer 1

A trigonograph (which can be considered a special case of this one, divided-through by $\cos\alpha\cos\beta\cos\gamma$):

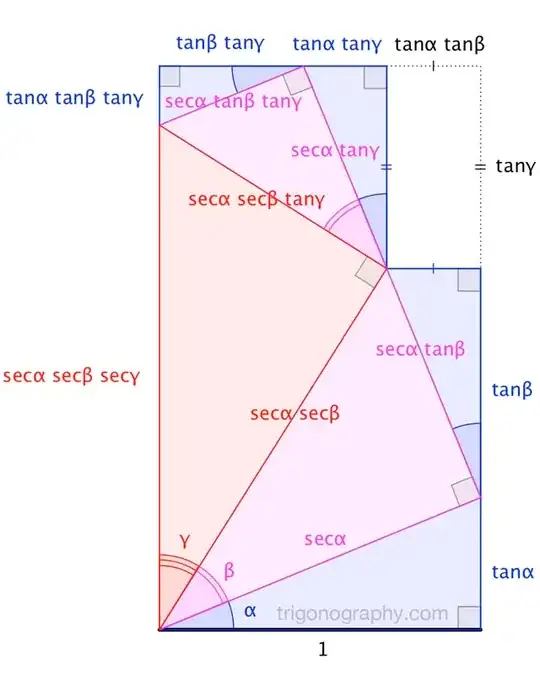
$$\alpha + \beta + \gamma = \frac{\pi}{2} \quad\implies\quad \begin{array}{c} \tan\alpha\tan\beta + \tan\beta \tan\gamma + \tan \gamma \tan \alpha = 1 \\[8pt] \tan\alpha + \tan \beta + \tan \gamma = \tan\alpha \tan\beta \tan\gamma + \sec\alpha \sec\beta \sec\gamma \end{array}$$

Answer 2

Using $\displaystyle \tan(A+B)=\dfrac{\tan A+\tan B}{1-\tan A\tan B},$

we can prove $$\tan(A+B+C)=\dfrac{\sum_\text{cyc}\tan A-\prod \tan A}{1-\sum_\text{cyc}\tan A\tan B}$$

$$\implies\cot(A+B+C)=\dfrac{1-\sum_\text{cyc}\tan A\tan B}{\sum_\text{cyc}\tan A-\prod \tan A}$$

If $A+B+C=\dfrac\pi2,\cot(A+B+C)=0$

Answer 3

HINT:

$$\arctan x+\arctan y=\dfrac\pi2-\arctan z$$

$$\tan\left(\arctan x+\arctan y\right)=\tan\left(\dfrac\pi2-\arctan z\right)$$

Use $\tan(\arctan z)=z$ and $\tan\left(\dfrac\pi2-\arctan z\right)=\tan(\text{arccot}z)$

If $\text{arccot}z=u,\cot u=z$ and $\tan(\text{arccot}z)=\tan u=\dfrac1z$

Answer 4

HINT:

$$\tan^{-1} x+\tan ^{-1}y= \pi/2-\tan^{-1}z $$

Take tan on both sides,

$$ \dfrac{x+y }{1- x y } = tan (RHS) = \dfrac{1}{z} $$

cross multiply, simplify.