3

Say you have $k$ i.i.d. normal random variables with some mean $\mu$ and variance $\sigma^2$ and you multiply them all together. What is the density function of the result?

Marius Kempe
  • 962

2 Answers2

6

Let $X_k = Z_1 Z_2 \cdots Z_k$, where $Z_i$ are iid normal r.v. with mean $\mu$ and variance $\sigma^2$. The precise density would be hard to come by, but moments are easy to compute: $$ \mathbb{E}(X_k^r) = \mathbb{E}(Z_1^r) \mathbb{E}(Z_2^r) \cdots \mathbb{E}(Z_k^r) = \left(m_r(Z)\right)^k $$

Here is some simulation in Mathematica:

ProductNormalHistogram[k_Integer?Positive, \[Mu]_, \[Sigma]_] := 
 Block[{x}, 
  Histogram[
   RandomVariate[
    TransformedDistribution[Array[x, k, 1, Times], 
     Array[x, k] \[Distributed] 
      ProductDistribution[{NormalDistribution[\[Mu], \[Sigma]
         ], k}]], 10^5], Automatic, "PDF", ImageSize -> 250]]

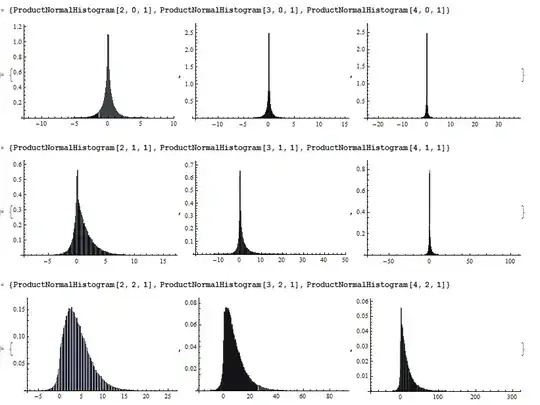
enter image description here

For the case of $\mu=0$ and $\sigma = 1$, look-up product-normal distribution for some analytic results.

Sasha
  • 70,631
4

I think this paper would interest you:

The Distribution of Products of Beta, Gamma and Gaussian Random Variables

M. D. Springer and W. E. Thompson
SIAM Journal on Applied Mathematics , Vol. 18, No. 4 (Jun., 1970), pp. 721-737

Published by: Society for Industrial and Applied Mathematics

Article Stable URL: http://www.jstor.org/stable/2099424

Hint--Elementary(!)

Prove that:

For continuous random variables $X$ and $Y$ with joint density $f$, the density of $Z=XY$ is given by $$f_Z(z)=\int_{-\infty}^\infty \frac 1 {|x|} f\left(x,\frac z x\right) \mathrm{d} x$$

Can you generalize this to $k$ of them by induction?

But, for me this looks like a far fetched idea in that, this is more elementary. (I have never had to bother about more than $2$ for computing by hand.)

Community
  • 1
  • This would probably take me about a week, not being a good mathematician - but I will do it! For now, could you tell me approximately what shape the result would have? – Marius Kempe Apr 19 '12 at 15:15
  • The result would leave you with a $\int\int\underbrace{\cdots}\int$ after changing the order of integration using Fubini...there would be $k$ integrals I guess. –  Apr 19 '12 at 15:22
  • Oh, I meant the visual shape of the resulting pdf when plotted. :-) – Marius Kempe Apr 19 '12 at 15:24
  • Not sure of that...sorry. –  Apr 19 '12 at 15:25
  • I have edited my answer to add a paper that might interest you. @MariusKempe –  Apr 19 '12 at 15:34