The ant's position at each time $n\in\mathbb{N}$ is a random variable which we could model in the complex plane as $Z_0=0$, $Z_n=Z_{n-1}+\Delta Z_n=\sum_{k-1}^n\Delta Z_k$ for moves $\Delta Z_n=e^{i\Theta_n}$ which are i.i.d. and which depend on uniform i.i.d. random variates $\Theta_n=2\pi\,U_n\sim\operatorname{Unif}\left(0,2\pi\right)$ .
If we also let
$$
R_n=|Z_n|\,,
\qquad
S_n=\sup\limits_{1\le k\le n}R_n
\qquad
\text{and}
\qquad
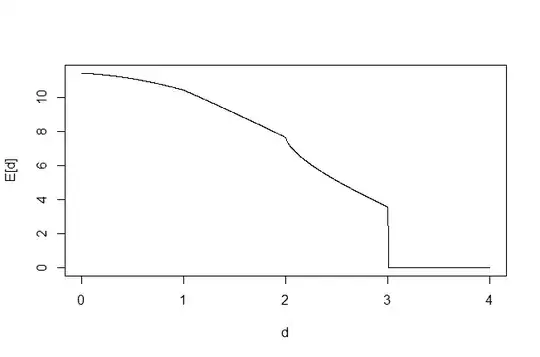
T=\inf\left\{n\mid R_n>R\right\}
$$
be the first time $n$ for which $R_n>R=3$,
then we are asking for $\mathbb{E}[T]$,
which can be calculated as
$$
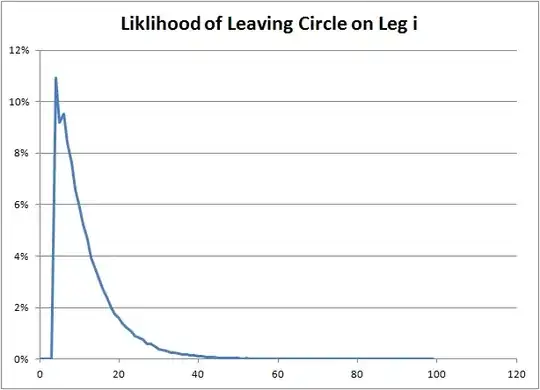
\mathbb{E}[T]=\sum_{n=R}^{\infty}n\cdot\mathbb{P}[R_{n-1} < R < R_n]\,.
$$
Now if we
let $F_n(r)=\mathbb{P}[R_n < r]$ and
let $f_n(r)=\mathbb{P}[R_n = r]$ be the PDF and CDF of $R_n$,
we can see that $F_n(n)=1$, and
we may be able to determine these functions inductively, with a recursion:
$$
\eqalign{
F_n(r)&=
\mathbb{P}[R_n < r]\\&=
\mathbb{P}[R_{n-1} < r-1]+
\mathbb{P}[R_n<r\,|\,r-1< R_{n-1}< r+1]
\\&=
F_{n-1}(r-1)+
\int_{r-1}^{r+1}
f_{n-1}(s)\cdot
\mathbb{P}[R_n<r|R_{n-1}=s]
\,ds
}
$$
The latter integral can certainly be split into the two cases
$s<r$ and $s>r$, for which the indeterminate probability inside
the integrand can be evaluated using geometry by subtracting
the area of sectors of circles (and triangles for $s>r$):
$$
\eqalign{
\mathbb{P}[R_n<r|R_{n-1}=s]&=
\left\{
\begin{align}
1-\frac{\beta -r^2 \alpha}{2\pi} && s \le r\\
\frac{A_\gamma+r^2A_\alpha}{2\pi} && s \gt r\\
\end{align}
\right.
}
$$
where the angles $\alpha,\beta,\gamma$
can be expressed using the law of cosines:
$$
\eqalign{
\cos\alpha &=\frac{r^2+s^2-1}{2rs}\\
\cos\beta &=\frac{r^2-s^2-1}{2 s}
\qquad\text{or}\qquad\sin\beta=r\,\sin\alpha\\
\cos\gamma &=\frac{-r^2+s^2+1}{2 s}=-\cos\beta\\
}
$$
(or solved from the equations
$re^{i\alpha}=s+e^{i\beta}$
& $\beta+\gamma=\pi$, from which one
can infer the diagrams for each case)
and $A_\alpha=2\alpha-\sin2\alpha$
is twice the area of
$\{z\in\mathbb{C}:\,|z|>r,\,|z-s|<1\}$.
Well, that's a start.
There is surely a more elegant recursion;
perhaps @carlop has found it.