7

Suppose that two ends of a cubic Bezier curve is connected by a straight line. Is there a simple way to find out whether this straight line intersects the Bezier curve (apart from the endpoints)? If it intersects then what will be the corresponding Bezier curve parameter's value?

John Railman
  • 165

2 Answers2

8

Given 2D cubic Bezier segment $\mathcal{B}(t,A,B,C,D)=A\,(1-t)^3+3B\,(1-t)^2t+3C\,(1-t)t^2+D\,t^3$, $t\in[0,1]$ and line segment $\mathcal{L}(t,A,D)=A\,(1-s)+D\,s$, $s\in[0,1]$, the value of $t:\mathcal{B}(t,A,B,C,D)=\mathcal{L}(s,A,D),\ t\ne0, t\ne1$ is the same as the value of $t:\mathcal{B}(t,0,B-A,C-A,D-A)=\mathcal{L}(s,0,D-A)$. So, with a substitution $b=B-A,\ c=C-A,\ d=D-A$ we can solve a system of two equations with two unknowns $t,s$:

\begin{align} \mathcal{B}(t,0,b_x,c_x,d_x) &= \mathcal{L}(s,0,d_x) \\ \mathcal{B}(t,0,b_y,c_y,d_y) &= \mathcal{L}(s,0,d_y) \end{align}

which gives the value of parameter $t$ as

\begin{align} t &= \frac{b_x\,d_y-d_x\,b_y}{b_x\,d_y-c_x\,d_y-d_x\,b_y+d_x\,c_y} \end{align}

If $0<t<1$ than the intersection point of $\mathcal{B}$ and $\mathcal{L}$ is $X=\mathcal{B}(t,A,B,C,D)$.

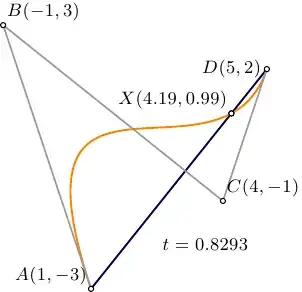
enter image description here

g.kov
  • 13,581
  • It is very explanatory and convincing, thanks. For a perfection I would like to propose a little algebraic correction: The line segment should be L(t,A,D). – John Railman Jun 24 '15 at 18:50
  • @John Railman: Of course it is $AD$, great thanks for pointing this, fixed. – g.kov Jun 24 '15 at 18:59
5

I just wanted to add to g.kov's good derivation, that the $t$ value is the parameter for the Bézier segment, not the line, so the range of $0 < t < 1$ stated above doesn't guarantee the the intersection is on the line segment between A and D, only that it is on the Bézier segment. The intersection could fall outside of the line segment, as pictured:

https://i.stack.imgur.com/ER2SH.png

Following the same substitution as above, $s$ can be derived as:

$$ s = \frac{\left(b_y d_x-b_x d_y\right) \left(d_x \left(3 b_x c_y^2-3 b_y c_x c_y-2 b_x b_y d_y\right)+d_y \left(-3 b_x c_x c_y+3 b_y c_x^2+b_x^2 d_y\right)+b_y^2 d_x^2\right)}{\left(d_x \left(b_y-c_y\right)+d_y \left(c_x-b_x\right)\right){}^3} $$

Only when both $0 < s < 1$ and $0 < t < 1$ is there point of intersection between the curve and line segment.

ddd
  • 53