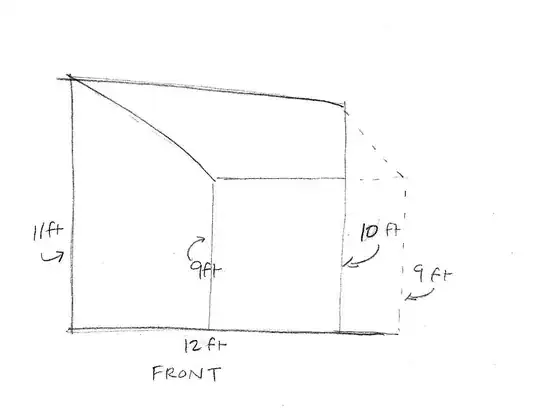
I get a total volume of around 16,654 cubit feet.
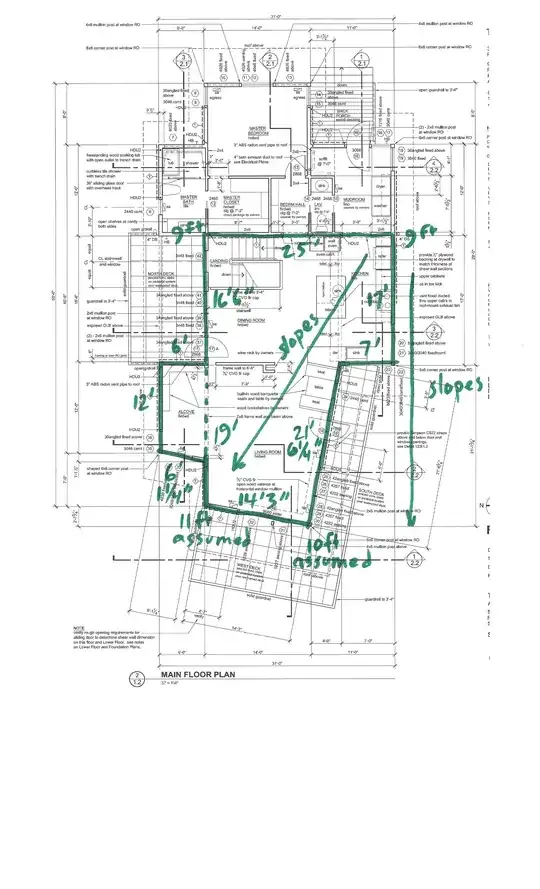
See my schematic:

Hopefully it's legible enough.
Basically, we put the floor onto a coordinate plane of our choosing. Since the upper right corner is the only right angle at an extreme of the room, I chose that as the origin.
We then find the coordinates of all the corners of the room, and express the height of the ceiling as a plane; the volume of the room is then the double integral over your floor plan of that plane.
The double integral is simplest when splitting into trapezoidal regions; I couldn't see how to use less than 4 (labeled $A,B,C,D$ on the graph).
We need to use the Pythagorean theorem to find the coordinates of two points: the bottom of region $B$ and the bottom of region $C$. The equations used are to the right of the schematic.
We solve for the plane describing the height of your ceiling by using the general formula for a plane, $f(x,y)=ax+by+c$ and plugging the three points whose heights we know to find $(a,b,c)$. If we use three points you told us: $(0,0,0), (-25,-35.5,11), (-11,-38.15,10)$, we get $(a,b,c)\approx(-.072,-.005,9)$, but this is inconsistent with your saying that we also have $(-25,0,9)$ (because $f(-25,0)\approx 11$). I'll assume the 9 is wrong, for now; the procedure from here is the same once we've figured out the plane for the height of the ceiling:
Finally, we integrate:
$$V=\intop\intop_A f(x,y)dydx+\intop\intop_{B}f(x,y)dydx+\intop\intop_{C}f(x,y)dydx+\intop\intop_D f(x,y)dydx$$
$$V=\intop_{-25}^0\intop_{-17}^0f(x,y)dydx+\intop_{-31}^{-25}\intop_{-.187x-34.29}^{-16.5}f(x,y)dydx+\intop_{-25}^{-11}\intop_{-40.23-.189x}^{-17}f(x,y)dydx+\intop_{-11}^{-7}\intop_{20.01+5.29x}^{-17}f(x,y)dydx$$
I plugged those integrals into Wolfram Alpha (e.g.) to get the final approximations and added them.
EDIT:
In fact, with some care taken we can get WolframAlpha to give us the answer in general in terms of the $(a,b,c)$ which describe your roof by using $\max$ and $\min$ to describe the lower boundary (otherwise the query is too long for the website):
$$V(a,b,c)=-12781.8a-13824.9b+820.356c$$
So once you settle on which heights to use to describe your roof, solve for $(a,b,c)$ and plug it in to that simple equation.