3

The Bring-Jerrard quintic,

$$x^5+x+t=0$$

can be solved as,

$$x = -\sum_{k=0}^\infty(-1)^k\frac{(5k)!}{k!(4k+1)!}\;t^{4k+1}\tag1$$

when,

$$|t|<\frac{4}{5^{5/4}}\approx 0.53\dots$$

This paper mentions how Passare and Tsikh found that a version of the principal quintic,

$$Bx^5+Ax^2+x+1 = 0$$

can be solved as,

$$x = -\sum_{j=0}^\infty \sum_{k=0}^\infty (-1)^k \frac{(2j+5k)!}{j!k!(j+4k+1)!}\;A^j B^k\tag2$$

The domain of convergence is, let $|A|,|B| = a,b$, then,

$$5^5b^2 - 4^4b + 108a^5 - 27a^4 + 1600a b - 2250a^2b<0$$

For example, let $A=173/5000,\;B=1/16$ and we find the series indeed yields $x=-0.9773\dots$

Question: Is there a double-sum solution like $(2)$ for the Bring-Jerrard sextic,

$$Bx^6+Ax^2+x+1=0$$

and if there is, what is its domain of convergence?

Community
  • 1
Tito Piezas III
  • 54,565

1 Answers1

4

If you write the equation as $x + 1 + t (c x^2 + d x^6) = 0$, then expand a root of this in powers of $t$, you get a series $$\eqalign{ x &= \sum_{n=0}^\infty C_n(c,d) t^n \cr &= -1 + (-c-d) t + (-2 c^2-8 c d-6 d^2) t^2 + \ldots }\tag{1}$$ where each $C_n(c,d)$ is a homogeneous polynomial of degree $n$ in $c,d$. For any $c,d$ this should converge for $t$ in some neighbourhood of $0$. The Lagrange inversion formula says $$\eqalign{C_n(c,d) &= \left.\dfrac{1}{n!} \left(\dfrac{d^{n-1}}{dx^{n-1}}\right) (-cx^2-dx^6)^n \right|_{x=-1}\cr &= - \sum_{j=0}^n \dfrac{(6n-4j)!}{ j! (n-j)! (5n-4j+1)!} c^j d^{n-j}}$$ That is, your double-sum formula is $$ x = - \sum_{j=0}^\infty \sum_{k=0}^\infty \dfrac{(2j+6k)!}{j! k! (j + 5 k + 1)!} A^j B^k \tag{2}$$

EDIT: The discriminant of $x+1 + t(cx^2 + d x^6)$ with respect to $x$ is $$-{d}^{3}{t}^{4} \left( 1024\,{c}^{6}{t}^{5}-256\,{c}^{5}{t}^{4}+13824 \,{c}^{3}d{t}^{3}-43200\,{c}^{2}d{t}^{2}+22500\,cdt+46656\,{d}^{2}t- 3125\,d \right) $$ Neglecting the factor $-d^3 t^4$ (which comes from the fact that when $t=0$ or $d=0$ the degree is less than $6$), the radius of convergence of the series (1) should be at least the smallest of the absolute values of roots of $1024\,{c}^{6}{t}^{5}-256\,{c}^{5}{t}^{4}+13824 \,{c}^{3}d{t}^{3}-43200\,{c}^{2}d{t}^{2}+22500\,cdt+46656\,{d}^{2}t- 3125\,d$ with respect to $t$. 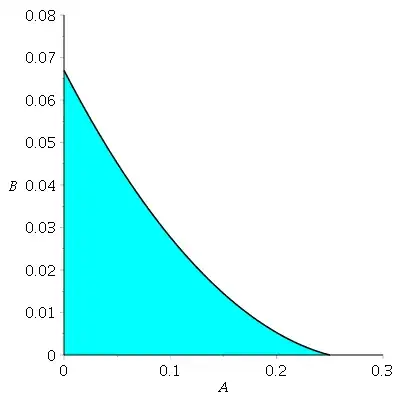In general I'm not sure this corresponds exactly to convergence of series (2) because of potential cancellations, but at least if $A,B > 0$ there are no cancellations to worry about. Thus we should have convergence of (2) at least in the shaded region of the first quadrant shown below, where the boundary curve is $-1024 A^6+256 A^5-13824 A^3 B+43200A^2 B-22500 A B-46656 B^2+3125 B = 0$.

enter image description here

Robert Israel
  • 448,999
  • Can you give an example of an $A,B$ that is within the domain of convergence? (I tested it with random $A,B$, but couldn't get the series for $x$ to be a root of the sextic.) – Tito Piezas III Jun 21 '15 at 12:47
  • Never mind, I found $A,B = 1/20,,1/100$ works. Correct me if I'm wrong, but is the domain of convergence given by $$-256 a^5 + 1024 a^6 + 3125 b - 22500 a b + 43200 a^2 b - 13824 a^3 b + 46656 b^2>0$$ where $|A|,|B| =a,b$? – Tito Piezas III Jun 21 '15 at 13:18
  • @TitoPiezasIII I think it should converge for $a=b=0$ and also when one of the parameter is fixed and the other gets large, your quantity gets to $+\infty$ so this is suspicious as well – mercio Jun 21 '15 at 14:27
  • Also I really believe that there should be a neighboorhood of $(0,0)$ where the series converges. – mercio Jun 21 '15 at 14:29
  • I can't for the life of me understand how to “expand a root of this in powers of t”. The best I can come up with is how expand $t=-\dfrac{x+1}{c~x^2+d~x^6}$ in powers of x, using the binomial series. – Lucian Jun 21 '15 at 14:32
  • @TitoPiezasIII I just tried to plot that for positive $a,b$ and I can't find any instance of negative values. Also, it is normal that the discriminant vanishes at $(0,0)$ because there are $4$ roots at infinity that get swapped around when you wiggle around it. But this doesn't change the root at $-1$ so it should be well-defined around $(0,0)$. I am not really quite certain what kind of shape we can have where the double sum is absolutely convergent, and my $4d$-vision is not really great so I don't know which part of the curve truely limits convergence. – mercio Jun 21 '15 at 15:00
  • @mercio: The domain of convergence for the Passare solution was the discriminant (up to some sign changes) of the quintic $Bx^5+Ax^2+x+1=0$. I simply assumed something similar for the sextic. You are right. I tested $A=1/20, B=5$ and it doesn't work, so that inequality must be modified. – Tito Piezas III Jun 21 '15 at 15:00
  • Also I'm completely amazed that the discirminant curve has genus $0$. There is a singularity where the surfaces crosses itself at one point and kinda um.. ties itself... – mercio Jun 21 '15 at 15:02
  • @mercio: Can we see the pic as a .png/.jpg file? – Tito Piezas III Jun 21 '15 at 15:08
  • @TitoPiezasIII : since (unlike the case in your paper) the coefficients all have the same sign, the series converge in a product of disks $D(r_a)*D(r_b)$ iff it converges for $a= +r_a,b = +r_b$. Now it should be easy to show that the convergence domain is delimited by the determinant curve for positive $a,b$ (and not positive $a$ and negative $b$) (also what picture do you want ?) – mercio Jun 21 '15 at 15:13
  • @mercio: That "...surface crosses itself at one point and kinda ties itself" thingie. I thought you were looking at a pic generated by some software. Also, if you figure out the explicit domain, kindly give it as an answer to supplement the one by Israel. – Tito Piezas III Jun 21 '15 at 15:19
  • @RobertIsrael How did you convert the $(6n-4j)!$ etc terms into factorials with only positive coefficients, like $(6k+2j)!$ ? – Тyma Gaidash Jan 16 '24 at 03:45
  • 1
    @ТymaGaidash If $n - j = k$, then $6n - 4 j = 2 j + 6 k$ and $5 n - 4 j = j + 5 k$. – Robert Israel Jan 16 '24 at 05:53