0

Let $X_1$ and $X_2$ be a random sample of size 2 from a uniform distribution over the interval $[0,1]$, let $Y_1$ and $Y_2$ be the corresponding order statistics. Find

  1. the conditional density function of $Y_1$ given $Y_2$
  2. the probability density function of $Y_2-Y_1$

I first had to find the order statistics of $Y_1$ which is $2(1-y)$ and of $Y_2$ which is $2y$. In both cases $0<y<1$. Should I use these two to find (1.)?

I also feel (2.) can only be done using convolution theorem of discrete random variables. Am I in the right direction?

zoli
  • 20,452
Dr. NGILAZI BANDA
  • 659

1 Answers1

4

We will need the joint comulatice distribution function $F_{Y_1,Y_2}(u,v)=P(Y_1<u,Y_2<v).$

Now,

$$P(Y_1<u,Y_2<v)=P(Y_1<u,Y_2<v, X_1\le X_2)+P(Y_1<u,Y_2<v ,X_2<X_1)=$$ $$=P(X_1<u,X_2<v, X_1\le X_2)+P(X_2<u,X_1<v ,X_2<X_1).$$

First, $$P(X_1<u,X_2<v, X_1\le X_2)= \begin{cases} -\frac{u^2}{2}+uv,&\text{ if }& 0\le u\le v \le 1\\ \frac{v^2}{2},&\text{ if }& 0\le v<u \le1 \end{cases}.$$

The figure below explains how I calculated the two pieces of surface area:

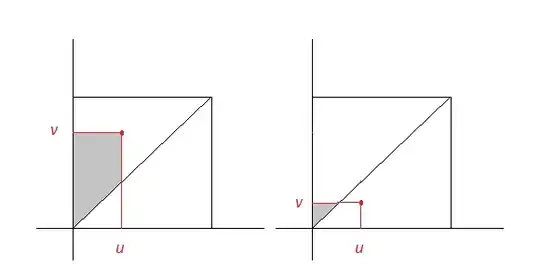
enter image description here

Second,

$$P(X_2<u,X_1<v ,X_2<X_1)=P(X_2<u,X_1<v, X_2\le X_1)= \begin{cases} -\frac{u^2}{2}+uv ,&\text{ if }& 0\le u\le v \le 1\\ \frac{v^2}{2},&\text{ if }& 0\le v<u \le1 \end{cases}.$$ (A figure similar to the one above would explain the latter result.) We can calculate the joint cdf: $$F_{Y_1,Y_2}(u,v)=$$$$=P(X_1<u,X_2<v, X_1\le X_2)+P(X_2<u,X_1<v ,X_2<X_1)=$$

$$=\begin{cases} -u^2+2uv,&\text{ if }& 0\le u\le v \le 1\\ v^2,&\text{ if }& 0\le v<u \le1 \end{cases}.$$

The joint pdf can be calculated the following way: $$f_{Y_1,Y_2}(u,v)=\frac{{\partial} ^2}{\partial u \partial v}F_{Y_1,Y_2}(u,v)=\begin{cases} 2,&\text{ if }& 0\le u\le v \le 1\\ 0,&\text{ otherwise. } \end{cases}$$

Then we will need the following marginal density:

$$f_{Y_2}(v)=\int_0^vf_{Y_1,Y_2}(u,v)du=2\int_0^v\ du=2v;\ 0\le v\le 1.$$

To answer the first question: By definition

$$f_{Y_1 \mid Y_2=v}(u)=\frac{f_{Y_1,Y_2}(u,v)}{f_{Y_2}(v)}=\begin{cases} \frac{1}{v},&\text{ if }& 0\le u\le v \le 1\\ 0,&\text{ else. } \end{cases} \tag 1$$

To answer the second question: First let's calculate the cdf of $Y_2-Y_1$. By definition

$$F_{Y_2-Y_1}(x)=P(Y_2-Y_1<x)=E[P(Y_2-Y_1<x \mid Y_2)]. $$

Then

$$P(Y_2-Y_1<x \mid Y_2=v)= \begin{cases} 0,&\text{ if } x<0\\ P(Y_1>v-x\mid Y_2=v),& \text{ if } 0\le x \le v \le 1\\ 1,&\text{ if } x>v \end{cases}$$

where $0\le v \le 1$.

Considering $(1)$ we have for $0\le x \le v \le 1$

$$P(Y_1>v-x\mid Y_2=v)=\frac 1v\int_{v-x}^v\ du=\frac xv.$$

So, for a given $0\le x \le 1$

$$P(Y_2-Y_1<x \mid Y_2=v)=\begin{cases} 1,& \text{ if } 0\le v\le x\\ \frac xv,&\text{ if } x\le v\le 1.\\ \end{cases}$$

As a result, for $0\le x \le 1$

$$F_{Y_2-Y_1}(x)=\int_0^1P(Y_2-Y_1<x \mid Y_2=v)f_{Y_2}(v)\ dv=$$ $$=2\int_0^x v \ dv + 2x\int_x^1 \ dv=2x-x^2.$$

Finally, $$f_{Y_2-Y_1}(x)=\begin{cases} 2-2x,& \text{ if } 0\le x \le 1 \\ 0,&\text{ otherwise. } \end{cases}$$

zoli
  • 20,452