I am having trouble understanding the answers here.
I am trying to prove that a compact subset of a Hausdorff space is closed.
Following the proof is difficult, perhaps because Brian reused letters for different things(although I get they are arbitrary, I can't follow it.) The second answer uses nets and filters, which I don't know of, so would like to avoid for now.
Now trying to follow Brians proof, I get something like the following:
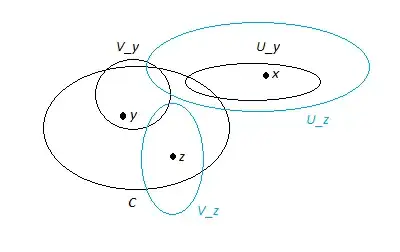
Let $S$ be our Hausdorff space, and $C\subset S$ be a compact subspace of $S$. (easy to remember, think $S$ for space, $C$ for compact)
To show that this subspace is closed, we can show the complement of the subspace is open. I.e. $S/C$ is open. Now following the proof of Brian, we take some element $x\in S/C$ and since $S$ is Hausdorff(which means $C$ is Hausdorff), we have for each $y\in C$ that there are disjoint open sets $U_y,V_y$ such that $x\in U_y$ and $y\in V_y$ now here is a little confusing, either he has reused $x$, or for some reason $x\in C$, which shouldn't be possible, since $x\in S/C$. Let's assume this is reusing the letter. Then the collection of all of these disjoint open sets, lets call it $\{\alpha_i,i\in C\}$ is an open cover of $C$, and since $C$ is compact, it has a finite subcover, $\{\alpha_i|u\in F\}$ where $F$ is a finite subset of $C$. Let $$U=\bigcap_{x\in F}V_y=\emptyset$$ Right? So then $U$ is open, since all empty sets are open... Now the proof doesn't even seem to follow.
I have no idea what's going on!