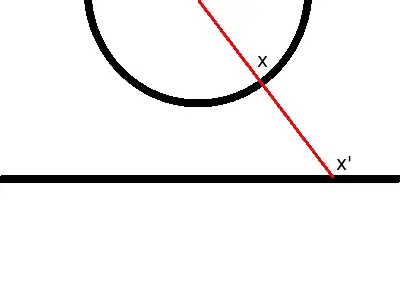
There are infinitely many real numbers between any two real numbers, therefore there are infinitely many real numbers in the range $[0,1]$ as there are in $[1, \infty)$. In a mathematical sense, are there more numbers in one range as opposed to the other? What about $[0,1]$ and $[0, \infty)$ ?
I'd assume this is akin to how limits work in that the limit as $x\to\infty$ of $\frac{x^x}{\log(x)}$ is $\infty$, even though both the numerator and denominator approach infinity.
The sets $[0,1]$ and $[1,\infty)$ have the same cardinality (i.e., there are exactly as many numbers in one as in the other). You can construct an explicit bijection between them with some tinkering on the tangent function (which provides a bijection between $[0,\pi/2)$ and $[0,+\infty)$).
In fact, you can easily construct a bijection between $[0,1)$ and $[1,\infty)$, which I suppose is sufficient for you at this point. It is more complicated to do it from $[0,1]$, see for example this question.
This isn't an answer to your exact question, but I think this picture really helped my intuition about this question:
On top we have a circle centered at, say, $(0,2)$ with radius one. Extend a radius through the circle until it hits the $x$-axis and we'll always get two points: $x$ and $x'$, in the graph.
Tracing out from left to right, we trace out both the semicircle and the whole $x$-axis, i.e. the real line.
But the former only has length $\pi$; with some rigor we can show that this means there are exactly as many numbers in and subset of the reals as there are reals.
The accepted answer is correct and answers your question perfectly.
You might read later in your education the sense in which $A:=[0,1]$ is almost finite while $B:=[1,\infty)$ is not. This almost finiteness is known as compactness and sets that are compact are in a different way smaller than non-compact sets.
For example, given any $\varepsilon>0$, you can quite easily find a finite number of elements of $A$, $\mathcal{C}:=\{x_1,x_2,\dots,x_N\}$ such that for all $x\in A$ there exists an $x_i\in \mathcal{C}$ such that
$$|x-x_i|<\varepsilon.$$
This is not the case for $B$.
You are a little confuse with the two concepts about infinity involve. The first one is about the "number of elements" in the sets. Each non degenerate interval has the same "number of elements" that other.
In the real line there are two types of infinity that counts "the numbers of elements". The first is named countable, this is the "number of elements" that has the natural numbers, and as the named said the intuitive idea is that you can count it. For example, the integers, an finite set, or the rational are countable.
The other concept is name no countable. The sets that are no countable has more elements than those who are countable. As and example each non degenerate interval is countable.
If you are interested in this topic you can read for example the third chapter of Analysis of Apostol.
The other concept involve is the infinity as a behavior, this means that as the variable get closer to some number the function gets greater, but the function itself is not infinity.
Another alternative:
There is an injection $[0,1] \to [1,\infty)$ given by $x \mapsto x + 1$. Hence the cardinalities $\|\,[0,1]\, \| \leq \|\,[1,\infty)\,\|$.
And there is an injection $[1,\infty) \to [0,1]$ given by $x \mapsto 1/x$. Hence $\|\, [1,\infty)\, \| \leq \|\,[0,1]\,\|$.
Therefore
$$\| [0,1] \| = \|[1,\infty)\|$$
Hint: Let $f(x)=\dfrac1x$ and $g(x)=\dfrac1{x+1}$ . Apply the former on $[1,\infty)$, and the latter on $[0,\infty)$.
