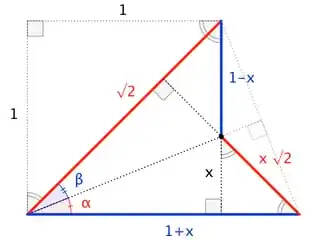
Here's another geometrical picture of what the identity means.
The tangent of an angle can also be interpreted as the slope of a line. That is, take a straight line through the origin of an XY cartesian coordinate system, then its equation in cartesian coordinates is
$$y=\tan{\theta} \; x$$
where $\theta$ is the angle between that line and the X-axis. There is however one line that does not fit in this scheme, but we're going to change that. Obviously, the Y-axis does not fit into that scheme because it's cartesian equation is $x=0$. We'll however extend our possible slopes with $\infty$ so that the Y-axis has slope $\infty$ and therefore $\tan \pi/2$ is defined to be $\infty$.
Now, going back to our cartesian plane, I want you to look at the following linear transformation
$$\mathbb{R}^2\to\mathbb{R}^2:\left(\begin{array}{c}x\\y\end{array}\right)\mapsto\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1 \\ 1 & -1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)$$
Since this is a linear transformation, it leaves the origin invariant but more than that it also maps straight lines through the origin to straight lines through the origin. Therefore, we can look to define it in terms of the slopes of these lines. Since the slope of a line is given by $z=y/x$ we have that
$$\mathbb{R}\cup \{\infty\}\to \mathbb{R}\cup \{\infty\} : z\mapsto\frac{1-z}{1+z}$$
This is exactly your transformation from before. Going back to my original linear transformation, we can check that it has eigenvalues $1$ and $-1$ with respective eigenvectors $(1,\sqrt{2}-1)$ and $(1,-\sqrt{2}-1)$. I've written those in such a way that we can immediately read off the slopes as $\sqrt{2}-1$ and $-\sqrt{2}-1$.
This indicates that our transformation is a reflection about the line with slope $\sqrt{2}-1$. This slope corresponds to an angle of $\pi/8$. Now, if I reflect an arbitrary line, the image of the line and the line both make an angle with the X-axis, the sum of which is $\pi/4$. You have to be careful in defining the angles for this to work, as the "orientation" of the line you reflect matters in defining the sign of the angle. Or you could work $\mod\pi$, which is a symmetry of the $\tan$ function anyway.
The transformation
$$\mathbb{C}\cup \{\infty\}\to \mathbb{C}\cup \{\infty\} : z\mapsto\frac{1-z}{1+z}$$
is also known as a Möbius transformation when it is working in the complex plane (or rather the Riemann sphere). But before that, they were also refered to as linear transformations, which at first may seem odd, because the prescription of the transformation is anything but linear. However, because of the connection I explicitly built up here with the group of linear transformations, it is more clear why the name is fitting. More precisely it is known that the group of Möbius transformations is related to the projective special linear group $PSL(2,\mathbb{C})$.
If I have more time, I'll try to look further into the geometric meaning of your identity in the context of the Riemann sphere.
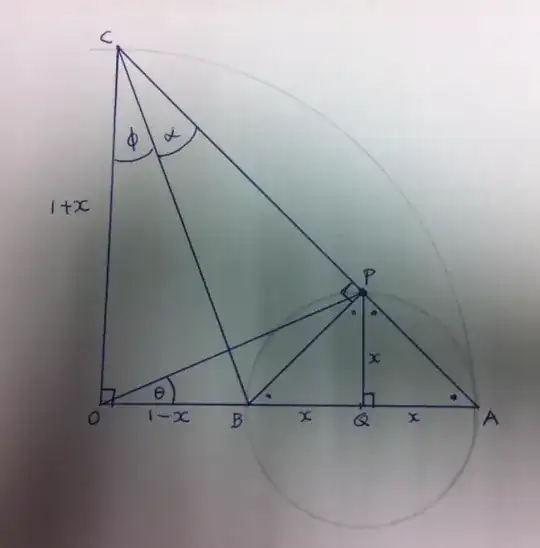
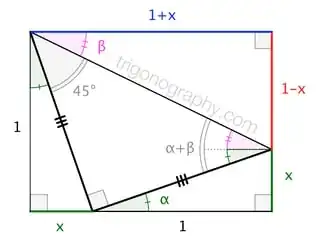
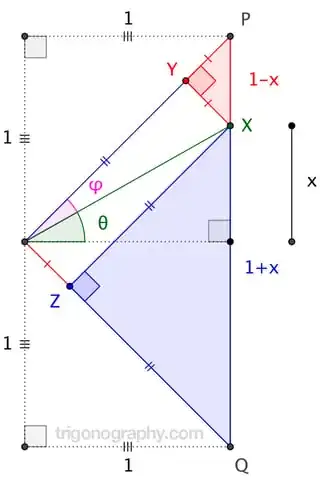
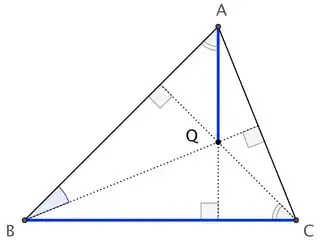
\frac a bsurprisingly hard to read, probably because I've never used it myself.) (What you didn't see was the edit I rejected, which had $\tan^{-1}$s everywhere... I fixed that, and then felt like neatening the whole thing.) – Chappers Jun 17 '15 at 17:19