Universal properties (again)

Question

I'm still trying to understand universal properties by understanding the definition of a free group $F_S$ over a set $S$. The diagram for the free group is this:

The diagram for an initial property looks like this:

Where $U : D \to C$ is a functor and according to Wikipedia an initial morphism from $X \in Obj(C)$ to $U$ is an initial object in the category of morphisms from $X$ to $U$.

First question: What happens to the second arrow in the second diagram for the free group? I assume $U(A)$ is $F_S$ and $U(Y)$ is $G$. So $U$ is probably a functor from sets to groups? Or what are $A$ and $Y$?

Second question: And what is a morphism from an object to a functor? I tried to find a definition but couldn't find one online. Can you explain to me what an initial morphism is?

Answer 1

The functor $U$ in this case is actually the forgetful functor from ${\rm Grp}$ to ${\rm Set}$, so $A=F_S$ and $U(A)$ is the underlying set of $F_S$; $Y=G$ and $U(Y)$ is the underlying set of $G$. Then if we read what the diagram says, for any object $Y$ in ${\rm Grp}$, there is a unique map $g$ from $A$ to $Y$ (in ${\rm Grp}$) such that $U(g)$ makes the stated diagram commute: exactly the definition of a free group on a set.

The second diagram disappears for the free group example because we can identify objects and morphisms with their images under $U$, with structure 'forgotten' in the image, and then simply add requirements to the objects ($G$ must be a group, $F_S$ must be a group, $\phi$ must be a group homomorphism).

Answer 2

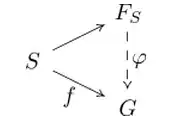
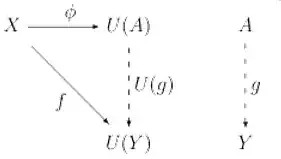
I think your problems are due to the fact that you are identifying groups with their underlying sets.

As you've pointed in the first diagram you have to see $F_S$ as $U(A)$ and $G$ as $U(Y)$, where $U$ is a functor of type

$$U \colon \mathbf{Grp} \to \mathbf{Set}$$

in particular this is the forgetful functor, which sends every group in its underlying set.

To complete the translation you have to see $\varphi$ as $U(g)$.

Definition of free groups using the first diagrams can avoid the use of functors because they usually state separately that $G$ and $F_S$ should have to be the underlying sets of some groups and that $\varphi$ should be a function that is also a group homomorphism. This statement is equivalent to requiring that there are some objects $A,Y \in \mathbf{Grp}$ and a morphism $g \in \mathbf{Grp}(A,Y)$ such that $U(A)=F_S$, $U(Y)=G$ and $\varphi=U(g)$.

Hope this explain how to see the first diagram as a special case of the second one.

For your second question, the wikipedia article you have linked has the answer to your question: suppose you have a functor between categories $\mathbf{C}$ and $\mathbf D$, let $U \colon \mathbf C \to \mathbf D$ be this functor, then a morphism from an object $X \in \mathbf D$ to the funtor $U$ is simply an object of the comma category $(\tilde X \downarrow U)$, while $\tilde X$ is the constant/selection functor for the object $X$. An initial morphism from $X$ to $U$ is just an initial object in the comma category $(\tilde X \downarrow U)$.

Edit: some specifications. The comma category $(\tilde X \downarrow U)$, where $U \colon \mathbf C \to \mathbf D$ is a functor and $X \in \mathbf D$, is the category having as set of objects the set $\bigcup_{Y \in \mathbb C} \mathbf D(X,U(Y))$, that is the set of all morphisms in $\mathbf D$ having $X$ as domain. Given two object is such category $u \colon X \to U(A)$ and $v \colon X \to U(B)$ a morphism $f \colon u \to v$ is a morphism $f \colon A \to B$ in $\mathbf C$ such that $v=U(f) \circ u$. The composition is inherited by $\mathbf C$ and so are the identities.

Hope this completely answer your question.

Answer 3

Your first diagram makes no sense, since it is mixing the category of Sets with the category of Groups (I guess $\varphi$ is a group morphism, while $S$ is only a set).

Let $U : Groups \to Sets$ be the forgetful functor.

What you are really looking for when you look for the free group over $S$, is a group $F_S$ together with a set morphism $i : S \to U(F_S)$ such that the applications $\phi_G : (g \in \hom_{Group}(F_S,G)) \mapsto (U(g) \circ i \in \hom_{Set}(S,U(G)))$ are all bijective : group morphisms from $F_S$ to a group $G$ correspond to set morphisms from $S$ to $G$ viewed as a set.
This is the universal property expressed in the second diagram : for every group $G$ and every set morphism $f : S \to U(G)$, there exists a unique group morphism $g : F_S \to G$ such that the diagram commutes ($U(g) \circ i = f$)

Define the category $C$ of morphisms from $S$ to $U$ to be the category whose objects are pairs $(G,f: S \to U(G))$ where $G$ is a group and $f$ is a set morphism, and whose morphisms from $(G_1,f_1)$ to $(G_2,f_2)$ are the group morphisms $g : G_1 \to G_2$ such that the diagram commutes ($U(g) \circ f_1 = f_2$).

Now we can translate in this context : we want a pair $(F_S,i)$, (we want an object $I$ of $C$), such that forall pair $(G,f)$ (forall object $X$ of $C$), there is a unique group morphism $g : F_S \to G$ such that $U(g) \circ i = f$ (there is a unique morphism $g : I \to X$ in $C$)