Is my constructive proof of the disjunctive syllogism principle correct?
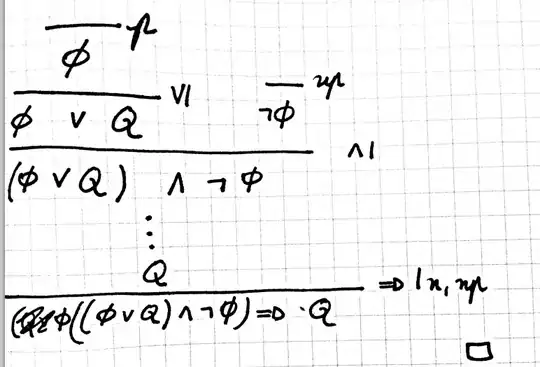
Is my constructive proof of the disjunctive syllogism principle correct?
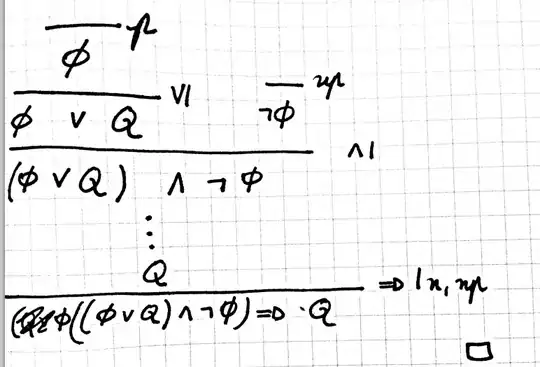
As suggested by Mohsen Shahriari, your derivation is not correct: to obtain a correct derivation you should explicit the rules used in the "vertical dots" part of your derivation.
The following is a derivation of $((\Phi \lor Q) \land \lnot \Phi) \to Q$ in intuitionistic (and hence "constructive") natural deduction.
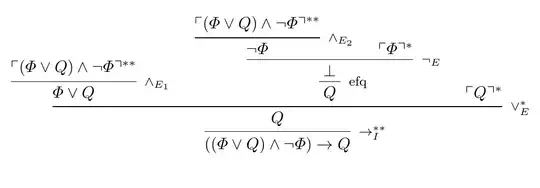
where efq is the rule ex falso quodlibet, also known as $\bot_E$, which is a rule of intuitionistic (and then classical) natural deduction but it not admissible in minimal natural deduction.