I am just curious to know the direct and precise to prove the identities
(1) $$\cos(A+B)=\cos A \cos B-\sin A \sin B$$ and
(2)
$$\sin(A+B)=\sin A \cos B+ \cos A \sin B$$ I tried to come up with right-angled triangles but I failed to connect them and get some logic out. Thank's in advance.
This was a nice geometric proof I learned when I took trig,
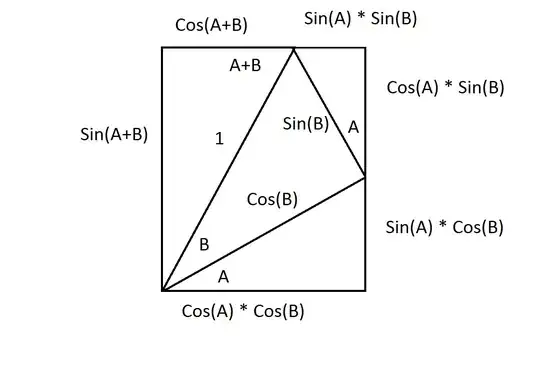
Take $A$ and $B$ on the unit circle, so that $A(\cos\theta;\sin\theta)$, $B(\cos\varphi;\sin\varphi)$.
Then $AB^2=(\cos\theta-\cos\varphi)^2+(\sin\theta-\sin\varphi)^2=2-2\cos\theta\cos\varphi-2\sin\theta\sin\varphi$
On the other hand, we apply the cosine rule to $\Delta AOB$, where $O$ is the origin: $AB^2=1^2+1^2-2\cdot 1\cdot 1\cos(\theta-\varphi)$. Hence the result
$$\cos(\theta-\varphi)=\cos\theta\cos\varphi+\sin\theta\sin\varphi$$
Then we derive $\cos\left(\frac{\pi}{2}-\varphi\right)=\sin\varphi$ and plug it into the other derived equation:
$$\begin{align}\sin(\theta-\varphi)&=\cos\left(\frac{\pi}{2}-\theta-(-\varphi)\right)\\&=\cos\left(\frac{\pi}{2}-\theta\right)\cos\varphi-\sin\left(\frac{\pi}{2}-\theta\right)\sin\varphi\\&=\sin\theta\cos\varphi-\cos\theta\sin\varphi\end{align}$$
To say, we can obtain the cosine rule without using that formulas.
How about using rotation matrices? $$R(\theta)=\left(\begin {matrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{matrix}\right)$$
Similarly for $\phi$ and use matrix multiplication. You get both $\sin(\theta+\phi)$ and $\cos(\theta+\phi)$ identities for the price of one!
