Trying to understand the true meaning of integral and Derivative in calculus

Question

I'm solving a physics question, and i just encountered some question i had no idea how to start, i just got the right answer and inside it it has something in math i never thought possible,

I know that the integral of $a$ (acceleration) by $t$ (time) will give me $v$ (velocity), I also know that the integral of $v$ by $t$ will give me $r$ or $x$ (the movement vector). I know that the derivative of $x$ will give me $v$, and the derivative of $v$ will give me $a$.

I just saw these few lines:

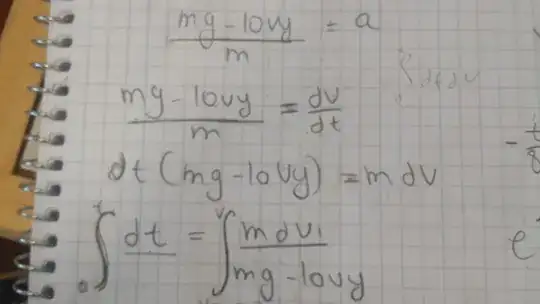
I somehow understand that you can replace $a$ with dv/dt because it's basically the same, but i have no idea how you can multiply the dt in the left sector of the equation, what does it mean?

I always thought that dx is basically saying 'Derivative by x' i never thought it's something "real" you can actually multiply and use basic math with...

Hope you could give me some idea about it, thanks!

In other answer i found this as the answer to "What does $dx$ mean?":

$dx$ does not mean anything. It's just a syntactical device to tell you the variable to differentiate with respect to or the integration variable.

This is exactly why i'm asking, because how can you multiply $dx$ in another thing if it's only a syntactical device?

Answer 1

$dx$ is called a differential. The notation is due to Leibniz and while the original meaning might have changed from being an infinitesimal quantity to a modern style differential, one still keeps the notation just because it allows to do some basic math on the differentials (like you wrote) and get reasonable results. Like the chain rule $$ \frac{df}{dx} = \frac{df}{du} \frac{du}{dx} $$ which you could write as $$ df = \frac{df}{du} \, du $$ and use it e.g. for solving an integral with substituion of variables $u = x^2$, $du = 2 x \, du$: $$ \int\limits_a^b x^2 dx = \int\limits_{a^2}^{b^2} u \frac{du}{2\sqrt{u}} = \frac{1}{2} \int\limits_{a^2}^{b^2} \sqrt{u} \, du $$ Or the total differential $$ df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial z} dz $$ Or the arc length of a curve in the $x$-$y$-plane: \begin{align} ds^2 &= dx^2 + dy^2 \Rightarrow \\ L &= \int\limits_1^2 ds \\ &= \int\limits_{x_1}^{x_2} \frac{ds}{dx} \, dx \\ &= \int\limits_{x_1}^{x_2} \frac{\sqrt{dx^2 + dy^2}}{dx} \, dx \\ &= \int\limits_{x_1}^{x_2} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \, dx \\ \end{align} In that sense the differentials and the rules used to manipulate differentials form a "Kalkül", a way to compute results. (I have only a German reference for this: link).

Answer 2

The technique being used here is called separation of variables. It can be done without separating differentials by using the chain rule. Specifically, you have (simplifying the notation a little bit)

$$\frac{dv}{dt} = \frac{mg - cv}{m}.$$

By dividing both sides by the expression on the right, you get

$$\frac{dv}{dt} \frac{m}{mg-cv} = 1.$$

Now integrate both sides where the time variable goes from $0$ to $t$:

$$\int_0^t \frac{dv}{ds} \frac{m}{mg-cv} ds = \int_0^t ds.$$

The annoying thing about doing it this way is that we have to introduce a new variable $s$ to use as the integration variable. But having done that, now you just need to integrate the left side by substitution, which can be justified by the chain rule and the fundamental theorem of calculus.

When you write this out with separation of differentials, you are essentially writing the syntactic result that happens after you change variables on the left side, and then taking the integration symbol away. That is, you get

$$\int_{v(0)}^{v(t)} \frac{m}{mg-cu} du = \int_0^t ds$$

which can be written in abbreviated form as

$$\frac{m dv}{mg-cv} = dt.$$

Answer 3

The issue is that the physics equations often use a finite difference approximation to a derivative: $$x'=\frac{dx}{dt}\approx\frac{\Delta x}{\Delta t}$$ Whenever $x$ is linear over the region of interest, that approximation is correct. In general, if the time-step ($\Delta t$) is small enough, then the linearity approximation does hold. In fact, this is the basis of how computers integrate differential equations. They approximate the next value of the function: $$x'(t)+g(t,x)*x(t)=h(t,x)$$ By doing this: $$x'(t)\approx \frac{\Delta x}{\Delta t} \approx h(t,x)-g(t,x)*x(t)$$ Step forward by providing a value for $\Delta t$: $$x_{new}(t)\approx x(t)+\Delta x=x(t)+(h(t,x)-g(t,x)*x)*\Delta t$$