What is the smallest unknown natural number?

Question

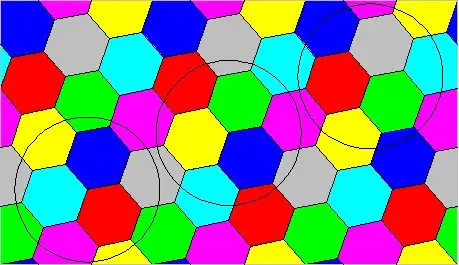
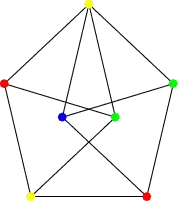
There are several unknown numbers in mathematics, such as optimal constants in some inequalities. Often it is enough to some estimates for these numbers from above and below, but finding the exact values is also interesting. There are situations where such unknown numbers are necessarily natural numbers, for example in Ramsey theory. For example, we know that there is a smallest integer $n$ such that any graph with $n$ vertices contains a complete or an independent subgraph of 10 vertices, but we don't know the exact value of $n$.

What kinds of unknown small (less than 100, say) integers are there? What are the smallest unknown constants which are known to be integers? Or, more rigorously, what is the smallest upper bound for an unknown but definable number that is known to be an integer?

I know that asking for the smallest unknown integer is ill-defined since we do not know the exact values. The more rigorous version of the question is well-posed, but I do not want to keep anyone from offering interesting examples even if they are clearly not going to win the race for the lowest upper bound.

An answer should contain a definition of an integer quantity (or a family of them) and known lower and upper bounds (both of which should be integers, not infinite). Conjectures about the actual value are also welcome. I have given one example below to give an idea of what I'm looking for.

Answer 1

The smallest infinitely often occurring prime gap, or

$$\liminf_{n\to\infty}\; (p_{n+1} - p_n)$$

is unknown as of now. Most likely, it is $2$, but the twin prime conjecture has not yet been settled.

Due to the work of Yitang Zhang and subsequent improvements by others (notably James Maynard and Terence Tao), we know that some prime gaps occur infinitely often. Zhang proved that gaps not larger than 70 million occur infinitely often, and the improvements lowered the bound to $246$ (perhaps there have been recent further improvements I'm not aware of).

Answer 2

The chromatic number $\chi$ of the plane satisfies $4 \le \chi \le 7$, i.e., $\chi \in \{4,5,6,7\}$. The problem is known as the Hadwiger-Nelson problem:

What is the minimum number of colors needed to color the plane such that no two points separated by a distance of exactly $1$ are assigned the same color?

The coloring below, due to John Isbell, shows that $\chi \le 7$:

---

         
          ^{(Image from mathpuzzle.com. The circles shown have unit radius.)}

---

And the 4-colorability of the unit-distance graph, the Moser Spindle, shows that $\chi \ge 4$:

---

         

---

Update (16 Apr 2018): Aubrey de Grey constructed a unit-distance graph of $1567$ vertices that has chromatic number $5$. See this post by Adam Goucher. This improves on the Moser spindle, and so now we know that $\chi \ge 5$, i.e., now $\chi \in \{5,6,7\}$.

---

     
      ^{de Grey, Aubrey DNJ. "The chromatic number of the plane is at least $5$." arXiv:1804.02385 (2018).}

---

Answer 3

How about the concrete problem of understanding how many (non-intersecting) spheres can touch another sphere in low dimensions? This is known as the kissing number problem, and it is open in dimension $5$.

In dimension $2$, the kissing number is $6$, given by the hexagonal tiling of the plane:

In dimension $3$, the kissing number is $12$, which is given by spheres at the vertices of the icosahedron. Note that there is actually so much extra space in dimension $3$ that we can swap any two spheres by continuous movement that leaves all the spheres non-intersecting and touching the central sphere. In dimension $4$ the optimal kissing number configuration has $24$ spheres, given by the vertices of the $24$-cell.

As for dimension $5$, all that is known is that it is at least $40$ and at most $44$. In fact the only other dimensions for which we know the value of the kissing number problem are $8$ and $24$, and this is due to the extraordinary symmetries of the $E_8$ and Leech lattices.

Answer 4

Ramsey numbers give the smallest sizes of graphs that ensure that certain kinds of subgroups of a given size can always be found. More specifically, $R(k,l)$ is the smallest integer such that any graph with at least so many vertices contains a complete subgraph of $k$ vertices or an independent subgraph of $l$ vertices.

Some small values are known, but there are surprisingly small unknown ones. For example:

• $36\leq R(4,6)\leq41$
• $43\leq R(5,5)\leq48$¹

The Electronic Journal of Combinatorics has a dynamical survey of small Ramsey numbers which you can consult for more details and newest bounds.

---

¹ At the time of writing this answer the limit was $49$. Vigleik Angeltveit and Brendan D. McKay released a preprint on March 26, 2017, proving $R(5,5)\leq 48$. The value has been updated in the dynamical survey as well. If there are changes to the relevant numbers in the survey, feel free to edit. (Other sources for updates can also be mentioned, but I will restrict the listed numbers to the values of the survey for consistence.)

Answer 5

Consider the following problem:

Find the smallest $n$ such that every number $k\geq3n$ with the same parity as $n$ can be written as the sum of $n$ odd primes.

• $n=1$ is trivially not true, because it states that every odd number is prime.
• For $n=2$ it is the Goldbach Conjecture.
• For $n=3$ it is the Weak Goldbach Conjecture, proven in 2013.

So the answer is in the set $\{2,3\}$.

Answer 6

How big is $2^{\aleph_\omega}$? ($\aleph_\omega$ is the $\omega$th uncountable cardinality.)

Of course, this question is well out of reach of ZFC, and certainly not about finite objects. However, Saharon Shelah showed that we can prove certain restrictions on this (and other) exponential quantities. In particular, he showed $$\text{If $2^{\aleph_k}<\aleph_\omega$ for every $k\in\omega$, then $2^{\aleph_\omega}<\aleph_{\omega_4}$.}$$

So far as I know the "4" is not known to be optimal, nor is there a good reason to believe it is apart from our inability to do better; see section 2 of Chapter IX of Shelah's book Cardinal Arithmetic, colorfully titled "Why the hell is it four?"

So here's an interesting unknown finite number:

What is the least $n$ such that ZFC proves: if $2^{\aleph_k}<\aleph_\omega$ for all $k\in\omega$, then $2^{\aleph_\omega}<\aleph_{\omega_n}$?

This may seem like a curiosity, but I think that computing this number - in particular, proving optimality, and reducing from 4 to something smaller if that's possible - would require fundamental advances in set theory.

Answer 7

Consider the value $$\max_{x \to \infty} \min \text{collatz}(x) . $$

Here, $\text{collatz}(x)$ for $x \in \mathbb{N}$ is defined as the set of generated numbers in the $3x + 1$-sequence in the Collatz conjecture when started from $x$.

Collatz conjecture is that $\max _{x \to \infty} \min \text{collatz}(x) = 1$

Answer 8

The value of $G(3)$ in the Waring's problem, or the upper bound to the number of cubes that are necessary to write a sufficiently large number.

Progress to this problem:

• Every number that is 4 or 5 mod 9 needs 4 cubes.
• It has been proven that 7 is enough by Linnik (1943).

Therefore $G(3)$ is a value form the set $\{4,5,6,7\}$.

---

Also, another thing related to Waring's problem:

What are the solutions to

$$2^k\{(3/2)^k\}+\lfloor (3/2)^k \rfloor > 2^k$$

Here $\{\}$ denotes the fractional part. It is conjectured that there are no solutions. It has been proven that there are only finitely many solutions.

Answer 9

Let me post another example.

What is the ninth solitary number?

It is known to be in the set $\{10,11\}$.

In fact, it is not know for any $k \geq 9$ what the $k$th solitary number is.

Answer 10

Which one of $\zeta (5),\zeta(7),\zeta(9),\zeta(11)$ is irrational. One of these were proven to be irrational, but it is not known which one out of the 4 are irrational.

Answer 11

The number of Fermat primes $F_n=2^{2^n}+1$.

One can easily check $F_0\to F_4$ are all primes. In history, it was conjectured that all these were prime. However, computational data shows that $F_5\to F_{30}$ are composite. Now it is conjectured that only the first $5$ are prime.

Answer 12

For any integer $N$, we can ask the following question: what is the smallest integer $k$ such that $\Sigma(k)>N$ (Busy Beaver function)? The answer is unknown for every $N\geq 4098$. For $N=4098$ the answer is either $5$ or $6$, and for, say, Graham's number, the answer is between $5$ and $22$.

Answer 13

Elliptic curves over $\mathbb Q$ of rank at least 28 are known, but their exact rank is not known.

Answer 14

As an alternative to unknown numbers that have a known "small" upper bound (e.g. $1$), or are otherwise likely to be small, here's one that is not very big but could (as far as we know) be fairly big, or not so big, or perhaps as small as $1$: $$\inf_{n\in\Bbb N}\left|\sum_{k=1}^{p+n}(-1)^k(p_{k+1}-p_k)\right|,$$where $p_k$ is the $k$th prime and $p=2^{57885161}-1$ is the largest known prime. (Here $p$ is chosen for ease of statement. Obviously there are numerous variations on this theme.)

Answer 15

The number $\pi$ has a very significant history and could be the ideal object of many problems about the first position in its decimal expansion in which a given property occurs.

In what position do the following properties occur first?

1. two consecutive twin numbers of two digits (six possible couples)

2. the number 5 appears 5 consecutive times

3. the first square of ten digits

4. Nothing is known about which digit appears countless times. However, it is clear that at least one digit does. What is this digit?

Many other similar questions can be formulated. Note that, excepting item 4, it is not obvious that there are corresponding answers but it is obvious also that their probability of existence is nonzero. A way to be sure of the existence of an answer is as follows:

The famous BBP Formula

$$\pi=\sum_{k=0}^\infty\left[\frac{1}{16^k}\left(\frac{4}{8k+1}-\frac{2}{8k+4}-\frac{1}{8k+5}-\frac{1}{8k+6}\right)\right]$$

gives the value of any position in the expansion of $\pi$ so one can look for some interesting property in an advanced position and ask about the minimal position at which this occurs. (It can be the discovered position, of course.)