What is the algorithm to generate the cards in the game "Dobble" ( known as "Spot it" in the USA )?h

Question

In the game Dobble ( known in the USA as "Spot it" ) , there is a pack of 55 playing cards, each with 8 different symbols on them. What is remarkable ( mathematically ) is that any two cards chosen at random from the pack will have one and only one matching symbol . This spurred me on to investigating the Maths behind generating such a pack of cards, starting with much more basic examples with only 2 symbols on each card and gradually working my way up to 8 .

This has been explored extensively in the linked question "What is the Math behind the game Spot it".

What has been established is that if the number of symbols on each card is N, then the maximum number of different symbols throughout the pack is C , the maximum number of cards in a pack is also C, the number of times any given symbol is repeated throughout the pack is N, and N and C are related as follows :

C = N^2 - N + 1 [ N squared minus N plus one ]

But I still do not understand the algorithm for generating the cards from a given symbol set .

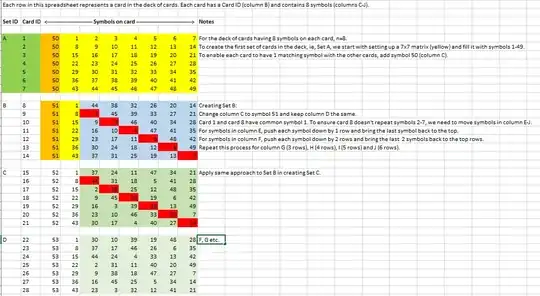
I am trying to follow the matrix generated by Don Simborg , but I just can't quite follow his formula . Even for a simple matrix with N=3 and C=7, I know what the matrix should look like , but can't seem to understand his descriptive syntax . For example in column 2, row 4, his formula suggests the symbol is the one numbered 3N-1 in the sequence of 7 symbols, but 3N-1= 8 , so which symbol should I use? Is he making an assumption that we just wrap around (subtract 7) and start counting again from the beginning of the sequence ? But this still generates the wrong symbol . I know from looking at the pattern that it should be either symbol no 4 or symbol no 5, but just can't see how this arises from his formula . If we take the 7 symbols as being the letters "A", "B", "C", "D", "E" and "F", then the matrix should be as follows below :

A B C

A D E

A F G

B D F

B E G

C D G

C E F

Can anyone help me? I've been trying to crack how to generate the symbol arrangements on the "Dobble" cards for months, and have succeeded in generating the sequence as far as N=6, C=31 but I am stuck at N=7 . I would welcome any assistance or enlightenment with this , thank you !

And if I have misunderstood Don Simborg's formula, then the error lies with me !

Here are the matrices I have found from my own trial and error :

For N=4, C=13, with a symbol set being A B C D E F G H I J K L M , the matrix is as follows :

A B C D

A E F G

A H I J

A K L M

B E H K

B F I L

B G J M

C E J L

C F H M

C G I K

D E I M

D F J K

D G H L

For N= 5, C = 21, with the symbol set : A B C D E F G H I J K L M N O P Q R S T U , the matrix is as follows :

A B C D E

A F G H I

A J K L M

A N O P Q

A R S T U

B F K N R

B G J O S

B H L P T

B I M Q U

C F J P U

C G K Q T

C H M N S

C I L O R

D F L Q S

D G M P R

D H K O U

D I J N T

E F M O T

E G L N U

E H J Q R

E I K P S

To state again, both the sets above have the remarkable quality that any two rows chosen at random will have one and only one matching symbol .

Answer 1

Here is an algorithm to generate a projective plane for every N prime. It will work for N power of prime if the computation of "(I*K + J) modulus N" below is made in the correct "field".

// N*N first cards
for I = 0 to N-1
   for J = 0 to N-1
      for K = 0 to N-1
         print ((I*K + J) modulus N)*N + K
      end for
      print N*N + I
      new line
   end for
end for

// N following cards
for I = 0 to N-1
   for J = 0 to N-1
      print J*N + I
   end for
   print N*N + N
   new line
end for

// Last card
for I = 0 to N-1
   print N*N + I
end for
new line

Answer 2

Here is a C code inspired from @karinka's answer with a different arrangement of symbols.

It works for $n$ being a prime number (2, 3, 5, 7, 11, 13, 17, ...).

Number of symbols in a given card = $n + 1$

Total number of cards = $n^2 + n + 1$

Total number of symbols = $n^2 + n + 1$

#include <stdio.h>
#include <stdlib.h>

#define PRINT(x) printf("%2d  ", (x)+1)

main() {
    int i, j, k, r = 0, n = 7;

    // first card
    printf ("Card %2d:  ", ++r);
    for (i = 0; i <= n; i++) {
        PRINT (i);
    }
    printf ("\n");

    // n following cards
    for (j = 0; j < n; j++) {
        printf ("Card %2d:  ", ++r);
        PRINT (0);
        for (k = 0; k < n; k++) {
            PRINT (n+1 + n*j + k);
        }
        printf ("\n");
    }

    // n*n following cards
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            printf ("Card %2d:  ", ++r);
            PRINT (i+1);
            for (k = 0; k < n; k++) {
                PRINT (n+1 + n*k + (i*k+j)%n); // Good for n = prime number
            }
            printf ("\n");
        }
    }
}

Example output with $n = 3$:

Card  1:   1   2   3   4
Card  2:   1   5   6   7
Card  3:   1   8   9  10
Card  4:   1  11  12  13
Card  5:   2   5   8  11
Card  6:   2   6   9  12
Card  7:   2   7  10  13
Card  8:   3   5   9  13
Card  9:   3   6  10  11
Card 10:   3   7   8  12
Card 11:   4   5  10  12
Card 12:   4   6   8  13
Card 13:   4   7   9  11

Answer 3

The generators submitted by Karinka, Urmil Karikh and Uwe are working nicely. However, original answer aimed at understanding the algorithm. The theory behind all three generators are in (See Paige L.J., Wexler Ch., A Canonical Form for Incidence Matrices of Projective Planes...., In Portugalie Mathematica, vol 12, fasc 3, 1953). It is generating Incidence matrix for projective plane of $q$th order in the normal form ($q=N-1$). Every row of incidence matrix corresponds to one card and column indexes where there are ones in the matrix, correspond to symbol on the card. Permutation Matrices, marked in the article as $C_{ij}$ are generated by cycling the identity matrix column-wise by $(i-1)(j-1) \mod q$ rows. This works only if $q$ is prime number, hence no divisors of zero exist in Galois field $GF(q)$. For $q$ not being prime, but only prime power, these permutation matrices $C_{ij}$ would have to be generated another way (i.e. neither addition nor multiplication groups of $GF(q)$ are not ordinary multiplication or addition, it has to be constructed using irreducible polynomials). So, above algorithms would not work for $q$ equal to $4$, $8$ or $9$. Anyway, from this matrix, you can nicely see that the two line (cards) has exactly one point (symbol) in common and vice-versa. Also, you can see that one symbol is on exactly $N$ cards and one card has exactly $N$ symbols (assuming that all 57 cards of Dobble would be printed and not only 55).

Answer 4

These help implementing @karinka's algorithm for p = 2^2 and p = 2^3 so you can easily get 4, 5, 6, 8 and 9 symbols per card for example. 10 symbols per card is also easy (p = 3^2) but there is no finite field of order 6 or 10, so 7 and 11 symbols per card cannot be generated (unless you allow more symbols than cards).

var GF4add = [
 [0, 1, 2, 3],
 [1, 0, 3, 2],
 [2, 3, 0, 1],
 [3, 2, 1, 0]
];

var GF4mul = [
 [0, 0, 0, 0],
 [0, 1, 2, 3],
 [0, 2, 3, 1],
 [0, 3, 1, 2]
];

var GF8add = [
 [0, 1, 2, 3, 4, 5, 6, 7],
 [1, 0, 3, 2, 5, 4, 7, 6],
 [2, 3, 0, 1, 6, 7, 4, 5],
 [3, 2, 1, 0, 7, 6, 5, 4],
 [4, 5, 6, 7, 0, 1, 2, 3],
 [5, 4, 7, 6, 1, 0, 3, 2],
 [6, 7, 4, 5, 2, 3, 0, 1],
 [7, 6, 5, 4, 3, 2, 1, 0]
];

var GF8mul = [
 [0, 0, 0, 0, 0, 0, 0, 0],
 [0, 1, 2, 3, 4, 5, 6, 7],
 [0, 2, 4, 6, 5, 7, 1, 3],
 [0, 3, 6, 5, 1, 2, 7, 4],
 [0, 4, 5, 1, 7, 3, 2, 6],
 [0, 5, 7, 2, 3, 6, 4, 1],
 [0, 6, 1, 7, 2, 4, 3, 5],
 [0, 7, 3, 4, 6, 1, 5, 2]
];

function mul(a, b, n)
{
    if (n == 4)
        return GF4mul[a][b];
    else if (n == 8)
        return GF8mul[a][b];
    else
        return (a * b) % n;
}

function add(a, b, n)
{
    if (n == 4)
        return GF4add[a][b];
    else if (n == 8)
        return GF8add[a][b];
    else
        return (a + b) % n;
}

Answer 5

@Karinka's answer in python:

def dobble(n):
    cards = []
    for i in range(n):
        for j in range(n):
            cards.append([(i*k + j) % n * n + k for k in range(n)] + [n*n + i])
    for i in range(n):
        cards.append([j * n + i for j in range(n)] + [n*n + n])
    cards.append([n * n + i for i in range(n+1)])
    return cards

from itertools import combinations
for card0, card1 in combinations(dobble(7), 2):
    assert len(set(card0) & set(card1)) == 1
```

Answer 6

in AutoIt:

$r=1
$n=7

ConsoleWrite("Card" & $r & "=")
for $i= 1 to $n+1
   ConsoleWrite(" " & $i )
Next
ConsoleWrite(@CRLF)
for $j=1 to $n
   $r=$r+1
   ConsoleWrite("Card" & $r & "=")
   ConsoleWrite(" 1")
   for $k=1 to $n
      ConsoleWrite(" " & $n + $n *($j-1) + $k+1 )
   Next
   ConsoleWrite(@crlf)
Next
for  $i= 1 to $n
   for $j=1 to $n
   $r=$r+1
   ConsoleWrite("Card" & $r & "=")
      ConsoleWrite(" " & $i+1 & " ")
   for $k=1 to $n
   ConsoleWrite($n + 2 + $n* ($k-1)  + mod(($i-1) *($k-1) +$j-1, $n) & " ")
      Next
      ConsoleWrite(@crlf)
   Next
Next


Result:
Card1= 1 2 3 4 5 6 7 8
Card2= 1 9 10 11 12 13 14 15
Card3= 1 16 17 18 19 20 21 22
Card4= 1 23 24 25 26 27 28 29
Card5= 1 30 31 32 33 34 35 36
Card6= 1 37 38 39 40 41 42 43
Card7= 1 44 45 46 47 48 49 50
Card8= 1 51 52 53 54 55 56 57
Card9= 2 9 16 23 30 37 44 51 
Card10= 2 10 17 24 31 38 45 52 
Card11= 2 11 18 25 32 39 46 53 
Card12= 2 12 19 26 33 40 47 54 
Card13= 2 13 20 27 34 41 48 55 
Card14= 2 14 21 28 35 42 49 56 
Card15= 2 15 22 29 36 43 50 57 
Card16= 3 9 17 25 33 41 49 57 
Card17= 3 10 18 26 34 42 50 51 
Card18= 3 11 19 27 35 43 44 52 
Card19= 3 12 20 28 36 37 45 53 
Card20= 3 13 21 29 30 38 46 54 
Card21= 3 14 22 23 31 39 47 55 
Card22= 3 15 16 24 32 40 48 56 
Card23= 4 9 18 27 36 38 47 56 
Card24= 4 10 19 28 30 39 48 57 
Card25= 4 11 20 29 31 40 49 51 
Card26= 4 12 21 23 32 41 50 52 
Card27= 4 13 22 24 33 42 44 53 
Card28= 4 14 16 25 34 43 45 54 
Card29= 4 15 17 26 35 37 46 55 
Card30= 5 9 19 29 32 42 45 55 
Card31= 5 10 20 23 33 43 46 56 
Card32= 5 11 21 24 34 37 47 57 
Card33= 5 12 22 25 35 38 48 51 
Card34= 5 13 16 26 36 39 49 52 
Card35= 5 14 17 27 30 40 50 53 
Card36= 5 15 18 28 31 41 44 54 
Card37= 6 9 20 24 35 39 50 54 
Card38= 6 10 21 25 36 40 44 55 
Card39= 6 11 22 26 30 41 45 56 
Card40= 6 12 16 27 31 42 46 57 
Card41= 6 13 17 28 32 43 47 51 
Card42= 6 14 18 29 33 37 48 52 
Card43= 6 15 19 23 34 38 49 53 
Card44= 7 9 21 26 31 43 48 53 
Card45= 7 10 22 27 32 37 49 54 
Card46= 7 11 16 28 33 38 50 55 
Card47= 7 12 17 29 34 39 44 56 
Card48= 7 13 18 23 35 40 45 57 
Card49= 7 14 19 24 36 41 46 51 
Card50= 7 15 20 25 30 42 47 52 
Card51= 8 9 22 28 34 40 46 52 
Card52= 8 10 16 29 35 41 47 53 
Card53= 8 11 17 23 36 42 48 54 
Card54= 8 12 18 24 30 43 49 55 
Card55= 8 13 19 25 31 37 50 56 
Card56= 8 14 20 26 32 38 44 57 
Card57= 8 15 21 27 33 39 45 51 

Answer 7

This is How I've converted the algorithm in javascript:

"use strict"

var i, j, k var r=1 var n=7

var res = ''; res = "Card" + r + "=" for (i = 1; i<= n+1; i++) { res += " " + i } console.log(res) for (j=1; j<=n; j++) { r=r+1 res = "Card" + r + "="; res += " 1"; for (k=1; k<=n; k++) { res += " " + (n + n * (j-1) + k+1) } console.log(res) } for (i= 1; i<=n; i++) { for (j=1; j<=n; j++) { r=r+1 res = "Card" + r + "=" res += " " + (i+1) + " " for (k=1; k<= n; k++) { res += n + 2 + n * (k-1) + (((i-1) * (k-1) +j-1) % n) + " " } console.log(res) } }

Answer 8

Dobble set for 5 symbols . Note that in cards 10 to 21, some of the indices cycle down whilst others cycle up. It was not possible to create a set if all the indices cycled in the same direction . I am still working on the Dobble set for 7 symbols .

Card 1 : 1, 2, 3, 4, 5

Card 2 : 1, 6, 7, 8, 9

Card 3 : 1, 10, 11, 12, 13

Card 4 : 1, 14, 15, 16, 17

Card 5 : 1, 18, 19, 20, 21

Card 6 : 2, 6, 10, 14, 18

Card 7 : 2, 7, 11, 15, 19

Card 8 : 2, 8, 12, 16, 20

Card 9 : 2, 9, 13, 17, 21

Card 10 : 3, 6, 11, 16, 21

Card 11 : 3, 7, 10, 17, 20

Card 12 : 3, 8, 13, 14, 19

Card 13 : 3, 9, 12, 15, 18

Card 14 : 4, 6, 12, 17, 19

Card 15 : 4, 7, 13, 16, 18

Card 16 : 4, 8, 10, 15, 21

Card 17 : 4, 9, 11, 14, 20

Card 18 : 5, 6, 13, 15, 20

Card 19 : 5, 7, 12, 14, 21

Card 20 : 5, 8, 11, 17, 18

Card 21 : 5, 9, 10, 16, 19

---

Below is a visualization of the pattern when there are 5 symbols per card from a set of 21 symbols and 21 cards.

Answer 9

Good thing I was able to write a program to check. the first listed failure are the lines

2     8    14    20    26    32    38
4     8    16    24    26    34    42

which overlap in the two numbers $8,26.$ Note that a projective plane of "order" $6$ is impossible. I was not $100\%$ sure that this list would amount to a projective plane, but I guess it does, therefore was doomed to failure.

I seem to have 7 symbols per card. I will need to write a computer program to compare the different cards. I found an algorithm, as I was doing this it seemed right, but maybe... Below see the $43$ cards, symbols are the numbers from $1$ to $43.$

$$ 1,2,3,4,5,6,7, $$ $$ 1,8,9,10,11,12,13,$$ $$ 1,14,15,16,17,18,19,$$ $$ 1,20,21,22,23,24,25, $$ $$ 1,26,27,28,29,30,31, $$ $$ 1,32,33,34,35,36,37, $$ $$ 1,38, 39,40,41,42,43,$$

$$ 2,8,14,20,26,32,38,$$ $$ 2,9,15,21,27,33,39,$$ $$ 2,10,16,22,28,34,40,$$ $$ 2,11,17,23,29,35,41,$$ $$ 2,12,18,24,30,36,42,$$ $$ 2,13,19,25,31,37,43,$$

$$ 3,8,15,22,29,36,43,$$ $$ 3,9,16,23,30,37,38,$$ $$ 3,10,17,24,31,32,39,$$ $$ 3,11,18,25,26,33,40,$$ $$ 3,12,19,20,27,34,41,$$ $$ 3,13,14,21,28,35,42,$$

$$ 4,8,16,24,26,34,42,$$ $$ 4,9,17,25,27,35,43,$$ $$ 4,10,18,20,28,36,38,$$ $$ 4,11,19,21,29,37,39,$$ $$ 4,12,14,22,30,32,40,$$ $$ 4,13,15,23,31,33,41,$$

$$ 5,8,17,20,29,32,41,$$ $$ 5,9,18,21,30,33,42,$$ $$ 5,10,19,22,31,34,43,$$ $$ 5,11,14,23,26,35,38,$$ $$ 5,12,15,24,27,36,39,$$ $$ 5,13,16,25,28,37,40,$$

$$ 6,8,18,22,26,36,40,$$ $$ 6,9,19,23,27,37,41,$$ $$ 6,10,14,24,28,32,42,$$ $$ 6,11,15,25,29,33,43,$$ $$ 6,12,16,20,30,34,38,$$ $$ 6,13,17,21,31,35,39,$$

$$ 7,8,19,24,29,34,39,$$ $$ 7,9,14,25,30,35,40,$$ $$ 7,10,15,20,31,36,41,$$ $$ 7,11,16,21,26,37,42,$$ $$ 7,12,17,22,27,32,43,$$ $$ 7,13,18,23,28,33,38,$$

Answer 10

Here is VBA code inspired from @karinka's and @Urmil Parikh answers but using an arrangement of symbols to match answers from @Urmil Parikh, @Uwe, and @Will Jagy.
You can swap the commented lines to print letters, though they won't match the pattern from the original question.

I realize there isn't anything new in my answer but I wanted to convert it to VBA so I could try out the code in an environment I have on hand, Excel. I'm hoping this can help someone else.

I don't quite grasp the comments about n being a prime number. This algorithm works when n is 4 or 8 (meaning 5 or 9 symbols per card).

Public Sub Generate()
' This will generate unique cards similar to "Spot it!" or "Dobble".

    Dim i, j, k, n, s, r

' How many symbols are on each card?
' Valid numbers are 3, 4, 6, 8, 12.  5, 7, and 11 will not generate correctly.
' If s is 5, cards 6 and 14 will match more than one card.
' If s is 7, cards 8, 20, and 26 will match more than one card for numbers 8, 20, 32
s = 4

    Debug.Print (s * s) - s + 1 & " unique cards will be generated with " & s & " symbols per card."

    n = s - 1 ' Reduce by 1 since all calcs are base 0.  n should be a prime number.

    Debug.Print "n=" & n

    '--- First card
    r = 1
    Debug.Print "Card " & r & ": ",
    For i = 0 To n
        Debug.Print i + 1;
        'Debug.Print Chr(i + 65), ' Alternative to print letters
    Next
    Debug.Print

    '--- N following cards
    For i = 0 To n - 1
        r = r + 1
        Debug.Print "Card " & r & ": ",
        Debug.Print 1;
        'Debug.Print "A",
        For j = 0 To n - 1
            Debug.Print n + 1 + (n * i) + j + 1;
            'Debug.Print Chr(n + 1 + (n * i) + j + 65), ' Alternative to print letters
        Next
        Debug.Print
    Next

    '--- N*N following cards
    For i = 0 To n - 1
        For j = 0 To n - 1
            r = r + 1
            Debug.Print "Card " & r & ": ",
            Debug.Print i + 2;
            'Debug.Print Chr(i + 66),
            For k = 0 To n - 1
                Debug.Print (n + 1) + (n * k) + ((i * k + j) Mod n) + 1;
                'Debug.Print Chr((n + 1) + (n * k) + ((i * k + j) Mod n) + 65), ' Alternative to print letters
            Next
            Debug.Print
        Next
    Next

End Sub

Sample output

13 unique cards will be generated with 4 symbols per card.
Card 1:        1  2  3  4 
Card 2:        1  5  6  7 
Card 3:        1  8  9  10 
Card 4:        1  11  12  13 
Card 5:        2  5  8  11 
Card 6:        2  6  9  12 
Card 7:        2  7  10  13 
Card 8:        3  5  9  13 
Card 9:        3  6  10  11 
Card 10:       3  7  8  12 
Card 11:       4  5  10  12 
Card 12:       4  6  8  13 
Card 13:       4  7  9  11 

7 unique cards will be generated with 3 symbols per card.
Card 1:       A             B             C             
Card 2:       A             D             E             
Card 3:       A             F             G             
Card 4:       B             D             F             
Card 5:       B             E             G             
Card 6:       C             D             G             
Card 7:       C             E             F          

vba excel-vba

Answer 11

Yesterday, I played the card game "Spot It" with my family and was facinated by the maths behind it. After working with my wife for a couple hours, we discovered the method to generate the cards. The method is now illustated using $8$ symbols per card.

Creating $49$ ($= 7$ sets of $7$) required cards:

Creating another set of $7$ using the matrix transpose:

the $57$th card:

The above method of construction can deal any number of symbols on the cards. It also shows that the maximum number of cards that meet the rules of the game is $57$, i.e. the same as the number of different symbols.

The general formula for the maximum number of cards with n symbols on each card satisfying the rules of the game is $(n-1)^2 + n$.