Problem.src) Evaluate $\displaystyle \int_{-\infty}^{\infty} \frac{x \sin x}{x^2+4} \, \mathrm{d}x $
I know I am supposed to split it up like this
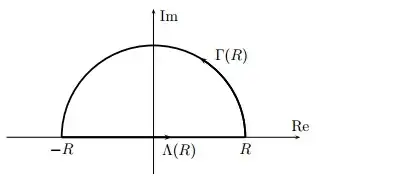
and $\Gamma(R)$ tends to zero and the other tends to my integral as $R$ tends to infinity?
I compute the residue at $2i$ which I think is $\frac{\sin(2i)}{2}$ ?
But I am a little stuck as to what to do now, I have never seen an example of this type of integral involving $\sin(x)$.
Usually we use the ML lemma for these types of problems, but because of the $x$ on top do I need to use Jordan's lemma?
Do I have to use $\sin(x)=\frac{e^{ix}-e^{-ix}}{2i}$ ? I am quite confused, any help would be appreciated.
Thanks.