2

Here is the proof of the Kolmogorov Zero-One Law and the lemmas used to prove it in Rosenthal's Probability book:

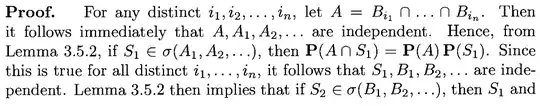
enter image description here enter image description here enter image description here

Here are my questions:

Question 1: In the first red box, does the fact that Q and P agree on J hold because of the statement in the blue box?

Question 2: What is the relevance of "independence is defined in terms of finite subcollections only" ? I was thinking that we can infer the independence of $A, A_1, A_2, ...$ merely from the $\forall n \in \mathbb{N}$.

Here is what I think "independence is defined in terms of finite subcollections only" means:

Given events $(A_n)_{n \geq 1}$, they are defined to be independent if for any indices $i_1, i_2, ..., i_n$,

$P(\bigcap_{k = i_1}^{i_n} A_{k}) = \prod_{k = i_1}^{i_n} P(A_{k})$.

Thus, the "finite subcollections" refers to the $A_{i_1}, A_{i_2}, ..., A_{i_n}$

Assuming I understood that right, how that is relevant?

BCLC
  • 13,459
  • 2
    For Question 1, the answer is "Yes". As for Question 2, what you say is OK; and it is relevant because any finite subcollection of $A, A_1, A_2,\dots$ is contained in $A,A_1, \dots ,A_{n-1}$ for some $n$. – Etienne May 24 '15 at 17:01
  • @Etienne Thanks. I think I get it now. Please correct me if I am wrong: if $\forall n \in \mathbb{N}, A, A_1, A_2, ... A_{n-1}$ are have a certain property, I think it does not follow that $A, A_1, A_2, ...$ have that same property similar to just because $\sum_{k \geq n \geq 1} a_n < \infty \forall k \in \mathbb{N}$ does not mean $\sum_{n \geq 1} a_n < \infty$. However, if that property is independence, then from the definition of independence, which includes your statement "any finite subcollection of A,A1,A2,… is contained in A,A1,…,An−1 for some n.", we can conclude such? – BCLC May 24 '15 at 18:05
  • 1
    @Etienne If so, how exactly can we conclude such? I sort of get it intuitively, I think but am unable to express it precisely. My guess: If $A, A_1, A_2, ..., A_{n-1}$ are independent, then any finite subcollection of that is independent. If this indeed holds $\forall n \in \mathbb{N}$, then finite subcollections of $A, A_1, A_2, ...$ are also independent. Hence, $A, A_1, A_2, ...$ is independent ? – BCLC May 24 '15 at 18:13
  • 2
    Yes, this is it. – Etienne May 24 '15 at 21:05
  • 1
    @Etienne Thanks! – BCLC May 28 '15 at 09:11
  • 2
    You're welcome! – Etienne May 29 '15 at 16:46

1 Answers1

0

For Question 1, the answer is "Yes". As for Question 2, what you say is OK; and it is relevant because any finite subcollection of A,A1,A2,… is contained in A,A1,…,An−1 for some n. – Etienne May 24 at 17:01

@Etienne Thanks. I think I get it now. Please correct me if I am wrong: if ∀n∈N,A,A1,A2,...An−1 are have a certain property, I think it does not follow that A,A1,A2,... have that same property similar to just because ∑k≥n≥1an<∞∀k∈N does not mean ∑n≥1an<∞. However, if that property is independence, then from the definition of independence, which includes your statement "any finite subcollection of A,A1,A2,… is contained in A,A1,…,An−1 for some n.", we can conclude such? – BCLC May 24 at 18:05

@Etienne If so, how exactly can we conclude such? I sort of get it intuitively, I think but am unable to express it precisely. My guess: If A,A1,A2,...,An−1 are independent, then any finite subcollection of that is independent. If this indeed holds ∀n∈N, then finite subcollections of A,A1,A2,... are also independent. Hence, A,A1,A2,... is independent ? – BCLC May 24 at 18:13

Yes, this is it. – Etienne May 24 at 21:05

@Etienne Thanks! – BCLC just now edit

BCLC
  • 13,459