On solvable quintics and septics

Question

Here is a nice sufficient (but not necessary) condition on whether a quintic is solvable in radicals or not. Given,

$x^5+10cx^3+10dx^2+5ex+f = 0\tag{1}$

If there is an ordering of its roots such that,

$x_1 x_2 + x_2 x_3 + x_3 x_4 + x_4 x_5 + x_5 x_1 - (x_1 x_3 + x_3 x_5 + x_5 x_2 + x_2 x_4 + x_4 x_1) = 0\tag{2}$

or alternatively, its coefficients are related by the quadratic in f,

$(c^3 + d^2 - c e) \big((5 c^2 - e)^2 + 16 c d^2\big) = (c^2 d + d e - c f)^2 \tag{3}$

then (1) is solvable. This also implies that if $c\neq0$, then it has a solvable twin,

$x^5+10cx^3+10dx^2+5ex+f' = 0\tag{4}$

where $f'$ is the other root of (3). The Lagrange resolvent are the roots of,

$z^4+fz^3+(2c^5-5c^3e-4d^2e+ce^2+2cdf)z^2-c^5fz+c^{10} = 0\tag{5}$

so,

$x = z_1^{1/5}+z_2^{1/5}+z_3^{1/5}+z_4^{1/5}\tag{6}$

Two questions though:

I. Does the septic (7th deg) analogue,

$x_1 x_2 + x_2 x_3 + \dots + x_7 x_1 – (x_1 x_3 + x_3 x_5 + \dots + x_6 x_1) = 0\tag{7}$

imply such a septic is solvable?

II. The septic has a $5! = 120$-deg resolvent. While this is next to impossible to explicitly construct, is it feasible to construct just the constant term? Equating it to zero would then imply a family of solvable septics, just like (3) above.

More details and examples for (2) like the Emma Lehmer quintic in my blog.

Answer 1

This problem is old but quite interesting. I have an answer to (I) which depends on some calculations in $\textsf{GAP}$ and Mathematica. I haven't thought about (II).

Suppose an irreducible septic has roots $x_1,\ldots,x_7$ that satisfy $$ x_1 x_2 + x_2 x_3 + \dots + x_7 x_1 – (x_1 x_3 + x_3 x_5 + \dots + x_6 x_1) = 0. $$ I claim that the Galois group is solvable.

Since the polynomial is irreducible, the Galois group must act transitively on the roots. Up to conjugacy, there are only seven transitive permutation groups of degree 7, of which only three are non-solvable. These are:

1. The symmetric group $S_7$.
2. The alternating group $A_7$.
3. The group $L(7) \cong \mathrm{PSL}(2,7)$ of symmetries of the Fano plane.

Since $L(7) \subset A_7 \subset S_7$, we can suppose that the Galois group contains a copy of $L(7)$ and attempt to derive a contradiction.

Now, the given identity involves a circular order on the seven roots of the septic. Up to symmetry, there are only three possible circular orders on the points of the Fano plane, corresponding to the three elements of $D_7\backslash S_7/L(7)$. (This result was computed in $\textsf{GAP}$.) Bijections of the Fano plane with $\{1,\ldots,7\}$ corresponding to these orders are shown below.

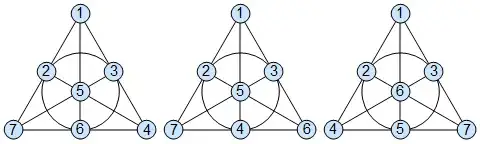
Thus, we may assume that the Galois group contains the symmetries of one of these three Fano planes.

Before tackling these cases individually, observe in general that the pointwise stabilizer of a line in the Fano plane is a Klein four-group, where every element is a product of two transpositions. For example, in the first plane, the symmetries that fix $1$, $2$, and $7$ are precisely $(3\;4)(5\;6)$, $(3\;5)(4\;6)$, and $(3\;6)(4\;5)$. These are the only sorts of elements of $L(7)$ that we will need for the argument.

Cases 1 and 2: In each of the first two planes, $\{3,5,7\}$ is a line, and thus $(1\;2)(4\;6)$ is an element of $L(7)$. Applying this permutation to the roots in the equation $$ x_1 x_2 + x_2 x_3 + \dots + x_7 x_1 – (x_1 x_3 + x_3 x_5 + \dots + x_6 x_1) = 0 $$ and subtracting from the original yields the equation $$ (2x_1-2x_2-x_4+x_6)(x_7-x_3) \;=\; 0. $$ Since $x_3\ne x_7$, we conclude that $2x_1 + x_6 = 2x_2+x_4$. Now, no three of $1,2,4,6$ are collinear in either of the first two planes. It follows that there is a symmetry of each of the planes that fixes $1$ and $6$ but switches $2$ and $4$, namely $(2\;4)(3\;7)$ for the first plane and $(2\;4)(5\;7)$ for the second plane. Thus we have two equations $$ 2x_1 + x_6 = 2x_2+x_4,\qquad 2x_1 + x_6 = x_2+2x_4, $$ and subtracting gives $x_2=x_4$, a contradiction.

Case 3: The argument for the last plane is similar but slightly more complicated. Observe that each of the following eight permutations is a symmetry of the third plane: $$ \text{the identity},\qquad (2\;7)(3\;4),\qquad (3\;6)(5\;7),\qquad (1\;3)(4\;5) $$ $$ (1\;2)(3\;6),\qquad (3\;7)(5\;6),\qquad (3\;5)(6\;7), \qquad (1\;2)(5\;7) $$ We apply each of these permutations to the equation $$ x_1 x_2 + x_2 x_3 + \dots + x_7 x_1 – (x_1 x_3 + x_3 x_5 + \dots + x_6 x_1) = 0, $$ adding together the first four results, and then subtracting the other four results. According to Mathematica, this gives the equation $$ 5(x_2-x_1)(x_3-x_5+x_6-x_7)=0. $$ Since $x_1\ne x_2$, it follows that $x_3+x_6=x_5+x_7$. As in the last case, observe that no three of $3,5,6,7$ are collinear, so there exists a symmetry of the plane that fixes $3$ and $5$ and switches $6$ and $7$, namely $(6\;7)(1\;4)$. This gives us two equations $$ x_3+x_6=x_5+x_7,\qquad x_3+x_7=x_5+x_6 $$ and subtracting yields $x_6=x_7$, a contradiction.

Answer 2

It turns out there is an infinite number of such septics, such as the Hashimoto-Hoshi septic, $$\small x^7 - (a^3 + a^2 + 5a + 6)x^6 + 3(3a^3 + 3a^2 + 8a + 4)x^5 + (a^7 + a^6 + 9a^5 - 5a^4 - 15a^3 - 22a^2 - 36a - 8)x^4 - a(a^7 + 5a^6 + 12a^5 + 24a^4 - 6a^3 + 2a^2 - 20a - 16)x^3 + a^2(2a^6 + 7a^5 + 19a^4 + 14a^3 + 2a^2 + 8a - 8)x^2 - a^4(a^4 + 4a^3 + 8a^2 + 4)x + a^7=0$$

For example, let $a=1$ so, $$1 - 17 x + 44 x^2 - 2 x^3 - 75 x^4 + 54 x^5 - 13 x^6 + x^7=0$$ which is the equation involved in $\cos\frac{\pi k}{43}$ and order its roots as, $$x_1,\,x_2,\,x_3,\,x_4,\,x_5,\,x_6,\,x_7 =\\ r_1,\,r_2,\,r_5,\,r_6,\,r_3,\,r_7,\,r_4 = \\ -0.752399,\; 0.0721331,\; 2.63744,\; 3.62599,\; 0.480671,\; 6.29991,\; 0.636246$$ where the $r_i$ is the root numbering in Mathematica. Then, $$ x_1 x_2 + x_2 x_3 + \dots + x_7 x_1 - (x_1 x_3 + x_3 x_5 + \dots + x_6 x_1) = 0$$