1

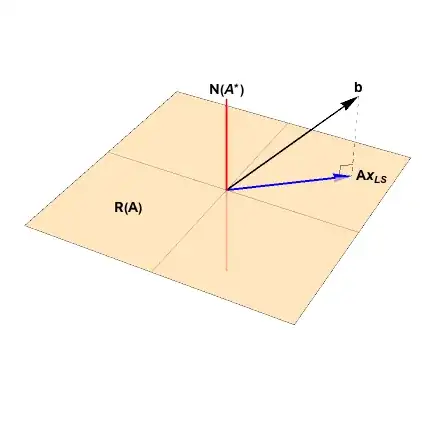
Let $b\in \mathbb{R}^m$,$A\in M_{m\times n}(\mathbb{R})$ with $m>n$ and $rank(A)=n$, and the element $x^*\in \mathbb{R}^m$ solution of least squares of $Ax=b$.

i) Show that $r^*=b-Ax^*\in N(A^T)$ where $N(A)$ denotes the null space.

ii) Find the pseudo-inverse of $A$ and warrants your answer

What I did

Let $z^*=Ax^*\in R(A)$, so by orthogonal decomposition theorem $b=z^*+r^*$ where $z^*\in R(A)$ and $r^*\in N(A^T)$ then $r^*=b-z^*=b-Ax^*$.

But in the part ii) I don't know how to do.

hmakholm left over Monica
  • 286,031
Roland
  • 3,165
  • 1
    Again $A^{-1}$ doesn't make any sense for non-square matrices! – Ehsan M. Kermani May 23 '15 at 02:12
  • do you mean that $x^* = A^{\dagger}b$, where $A^{\dagger}$ is the pseudoinverse of $A$? – etothepitimesi May 23 '15 at 02:37
  • @el.Salvador I made a mistake, $x^*$ it's just the solution of least squares – Roland May 23 '15 at 02:42
  • @askazy, the solution of $Ax=b$ in the least squares sense is exactly $x^* = A^{\dagger}b$. – etothepitimesi May 23 '15 at 02:45
  • Please stop using the tag "self-learning" in all your questions. That tag is for questions that is about how to self-study. Just because you came across a problem while reading something of your own does not mean that the problem is about self-learning. – hmakholm left over Monica May 23 '15 at 14:12
  • This post derives the pseudoinverse solution for the least squares problem: http://math.stackexchange.com/questions/772039/proving-standard-least-square-problem-with-svd/2173715#2173715. – dantopa Mar 06 '17 at 21:26

2 Answers2

2

you can show that $rank(A^\top A) = rank(A) = n.$ define $x^* = (A^\top A)^{-1}A^\top b$ that is $A^\top A x^* = A^\top b.$ the pseudo inverse of $A$ is $(A^\top A)^{-1}A^\top.$

abel
  • 29,170
1

1 Given the general least squares problem, $$ \lVert \mathbf{A} x - b \rVert_{2}^{2} > 0 $$ and the constraint $$ \lVert \mathbf{A} x - b \rVert_{2}^{2} < \lVert b \rVert_{2}^{2} $$ ($b$ is not in the null space), we can decompose the problem as $$ \color{blue}{\mathbf{A}x} = \color{blue}{{b}_{\mathcal{R}\left( \mathbf{A} \right)}} + \color{red} {{b}_{\mathcal{N}\left( \mathbf{A}^{*} \right)}}. $$ This resolves the data vector into its $\color{blue}{range}$ space and $\color{red}{nullspace}$ components. The derivation is shown in How does the SVD solve the least squares problem?

The residual error vector is the component of the data vector which resides in the null space: $$ \color{red}{r\left(x_{LS}\right)} = \color{blue}{\mathbf{A}x} - ( \color{blue}{{b}_{\mathcal{R}\left( \mathbf{A} \right)}} - \color{red} {{b}_{\mathcal{N}\left( \mathbf{A}^{*} \right)}}) = \color{red} {{b}_{\mathcal{N}\left( \mathbf{A}^{*} \right)}} $$

Resolving the data vector into range and null space components.

2 The aforementioned post may be your answer.

dantopa
  • 10,342