Setting polynomials to zero: basic math question: $(x-4)^2$

Question

I am little confused when I set this polynomial to zero what does the result mean? Does the parabola have a minimum point at $4$?

Answer 1

The main points here are that:

1) $\color{red}{\text{stuff}}^2=0 \iff \color{red}{\text{stuff}} = 0$.

2) $\color{red}{\text{stuff}}^2 \geq 0$ always, if $\color{red}{\rm stuff}$ is a real number.

Applying this here: by (1), $(x-4)^2 \geq 0$ for all $x \in \Bbb R$. By (2), the minimum value will happen if and only if $(x-4)^2 = 0$, that is, if and only if $x-4=0$. So the function attains a minimum, which is zero, for $x=4$, and only for this value.

Answer 2

You have \begin{align} y=\left(x-4\right)^2.\tag{1} \end{align} What we could also do is write it as \begin{align} y&=\left(x-4\right)\left(x-4\right)\\ &=x^2-4x-4x+16\\ &=x^2-8x+16.\tag{2} \end{align} Now, we'll stop and take a look at $\left(2\right)$ for a bit. Notice I have set it $=$ to another variable $y$. I've done this because $\left(2\right)$ varies in the $y$ direction as we change our input $x$ (sometimes called a "free variable"). $y$ is then the dependent variable since it depends upon our input $x$. We might then write it as \begin{align} y=f\left(x\right)&=x^2-8x+16,\tag{3} \end{align} since $\left(3\right)$ is indeed a function of $x$. Now if we set $\left(3\right)$ equal to a definite number, like $0$, we are finding those values of $x$ that result in that fixed value. In this case we can use the quadratic formula to find those values: \begin{align} 0&=x^2-8x+16\\ \implies x&=\frac{8\pm\sqrt{64-4\left(1\right)\left(16\right)}}{2}\\ &=4.\tag{4} \end{align} I would highly recommend you take a look here to see how I have found $x$. Here is a graph of $\left(1\right)$ for a visual aid before I continue (the blue curve):

In this specific instance, the roots of the quadratic are indeed the minimum. You will find that in the quadratic formula, more generally written as \begin{align} x&=\color{red}{\frac{-B}{2A}}\pm\color{blue}{\frac{\sqrt{B^2-4AC}}{2A}}\tag{5} \end{align} for a quadratic \begin{align} y=f\left(x\right)&=Ax^2+Bx+C,\tag{6} \end{align} the red part of $\left(5\right)$ finds the $x$-value of the vertex of the parabola, whereas the latter blue portion adds and subtracts the $x$-distance along the $x$-axis our roots are from the $x$ value of the vertex. Notice that in $\left(4\right)$ the "adding and subtracting" blue portion disappeared since the radical was $0$. Hence, the vertex and double-root of $\left(1\right)$, your problem, are at the same point. The parabola thus is sitting directly on the $x$-axis, which is apparent in the above plot.

Once you have seen enough functions like $y=\left(x-4\right)^2$ you will notice immediately that the parabola's roots and vertex are at the same point $\left(4,0\right)$ since this is the same as shifting the graph of $y=x^2$ to the right four units by the "substitution" $x=x-4$.

If you would like to locate the minimums of a function like $\left(1\right)$ you may use the concept of derivatives typically covered in introductory Calculus courses.

Answer 3

What it means is that it just barely touches the x-axis. And as that is the only real root the equation can have it means it doesn't move past or through the x-axis and that it therefore is the minimum point of the parabola.

Answer 4

assuming $y=polynomial(x)$ (in this case $y=(x-4)^2$).

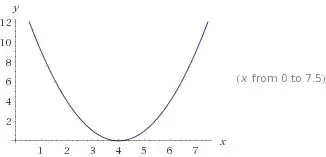
Setting a polynomial to zero or finding a root is finding a $x$ that makes $y=0$. Since $(4-4)^2=0^2=0$ , $y=0$ only when $x=4$.

Note that finding a root is not always equivalent to finding a minimum point of the polynomial. For example if $y=(x-1)(x-4)$:

You can see that this polynomial has 2 roots and that none of them is the minimal point. In fact not all polynomials have a minimal point. See this one $(x-2)(x-4)^2$.

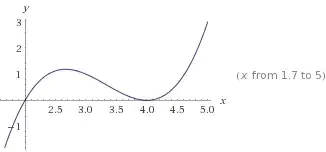
The fact the polynomial $(x-4)^2$ has a single root and this one is also the minimal point is due to the properties of parabolas.