Let $a_j\in \mathbb{N}$, with $0< a_{j-1}<a_j$. My question is:
What is known about the counting functions $\sigma_{k,p}(n)$, counting how many numbers, less than $n$, have a decomposition into a sum of $k$ $p$-powers of $a_j$?
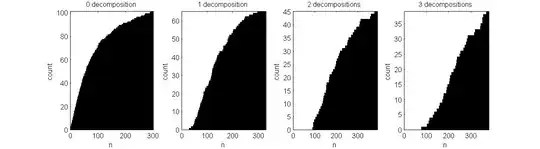
So for every $x\le n$, I ask, how many ways there are to decompose $x$ like $$ x=\sum_{j=1}^{k} a_j^p, $$ and then sum these (ways) up, e.g. $30$ has a unique decomposition into $1^2+2^2+3^2+4^2$, $90$ has 2 ($1^2+2^2+6^2+7^2$ and $1^2+3^2+4^2+8^2$), $78$ has 3 (see here) and so forth...
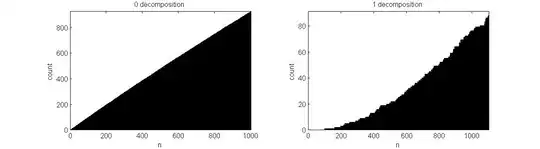
Below you'll find some plots, where I summed up $4$ squares with $\max a_j=300$ and $4$ cubes with $\max a_j=200$.
They show a quite different behaviour, concerning their curvature, but I'm not sure if this is an artifact of the sample I have taken.
EDIT: The linear appearance of the lower left cube-plot might be related to the fact that even if $a_j=a_k$ is allowed (Waring's problem) $9$ cubes are needed to represent all numbers. So does the curvature related to the number of $p$ powers I add up?