$\, a\bmod n\ $ and $\,a\, \%\, n\,$ are operations that denote the remainder $\,r\,$ left when dividing $\, a\,$ by $\,n\,$ using the (Euclidean) integer division algorithm: $\ a = q\, n + r\,$ with quotient $\:\!q\:\!$ and remainder $\:\!r.\,$ For naturals $\,a,n\,$ the remainder is usually normalized so $\,0\le r< n,\,$ Alternative to remainders we can use as normal forms any complete set of residues $\!\bmod n,\,$ i.e. any set of integers such that every integer is congruent to exactly one element of the set (i.e. a set of irredundant representatives for every congruence class), e.g. $\!\bmod 5\,$ we can use least magnitude reps $\,0,\pm1, \pm2\ $ (here $\,4\bmod 5 = -1)$ or, more generally, any $5$ consecutive integers.
Normal form reps allow us to reduce testing congruence to testing equality of normal forms (similar to testing fraction equivalence by testing equality of their least term reductions), i.e.
$$\begin{align} a\equiv b\!\!\!\pmod{\!n}&\iff a\bmod n = b\bmod n\\[.3em]
{\rm like}\quad\ \frac{a}c \,\equiv\, \frac{b}d &\iff \ell\left[\frac{a}c\right]\, =\, \ell\left[\frac{b}d\right],\ \ \ell = \text{least_terms}\end{align}\qquad$$
Recall the congruence relation $\,a\equiv b\pmod{\!n}\,$ means $\,n\mid a-b,\,$ i.e. $\,n\,$ divides $\,a-b.\,$ Take care not to confuse this $\!\bmod\!$ relation with the above operation (see here for more on such).
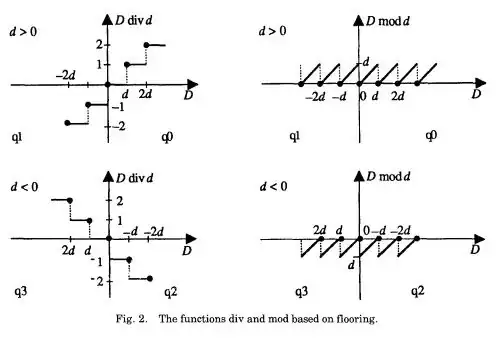
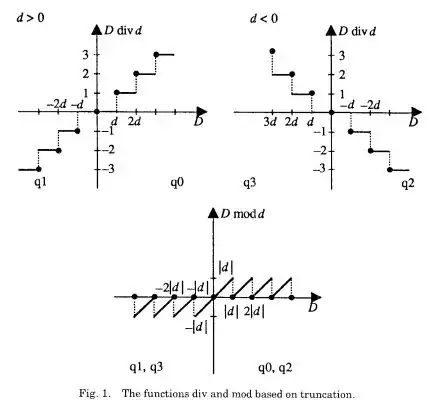
There are various conventions in use that specify how to define the quotient and remainder for the division algorithm when extending the above from naturals to integers, i.e. allowing negative integers. The remainder is uniquely determined once one defines the quotient, so usually the conventions say which way to round the quotient, e.g. towards $\,0\,$ or towards the nearest integer or towards $\pm\infty.$ Some programming languages provide all of the possibilities, e.g. see the floor, ceiling, round, truncate functions in Common Lisp.
The conventions always satisfy $\ a\bmod n \equiv a\,\pmod{\!n},\ $ i.e. the normal form of $\,a\,$ is an element of the congruence equivalence class $\, a+n\Bbb Z\,$ of all integers congruent to $\,a,\,$ so normal form reduction is compatible with modular arithmetic $\bmod n.\,$ Generally we can replace an argument of a sum or product (but not exponent) by any congruent integer and we obtain a congruent result, by the Congruence Sum & Product Rules, or their inductive extension: the Congruence Polynomial Rule. When performing modular computation this property allows us to use our ingenuity to choose (non-normal) reps that simplify the calculation, e.g. using $\,-1\,$ vs. $\,9\,$ when computing $\,9^{2n}\bmod 10.\,$ But machines generally lack such ingenuity - they are programmed using deterministic algorithms so they must use a modular reduction operation $\,a\,\mapsto\, a\bmod n.$
A web search will turn up further discussion of such conventions in many places, e.g. on Wikipedia and D. Leijen, Division and Modulus for Computer Scientists., and R. Boute, The Euclidean Definition of the Functions div
and mod, which includes the following figures