Hint:
Let (symbol) denote the event of (event)
As - Assault
R - Report
A - Arrested
C - Conviction
S - Serving
We know ( Note that | means given)
P(R|As) = 0.5
P(A|R) = 0.6
P(C|A) = 0.9
P(S|C) = 0.7
and
We want to know:
P(S|As) = ?
Before computing this mathematically, through conditional probability, let us think about this intuitively using probability tree diagrams.
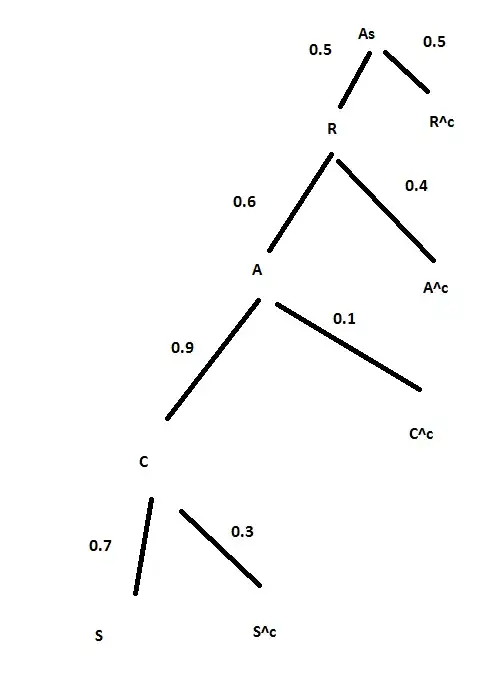
anything with "^c" means complement as in the event did not occur e.g. R^c ($R^c$) means that the assault was not reported.
It seems that the only way to arrive at S from As is through R, A, C and S. This is correct as unreported assaults do not result in arrests, not being arrested cannot result in a conviction and not being convicted means not serving.
When going through the probability tree this way, we multiply the probabilities (eg the probability of getting double 6's when rolling a pair of fair dice is (1/6)*(1/6) = 1/36).
Thus, the answer would be 0.5*0.6*0.9*0.7, but how do we state this formally? More importantly, why does going through the probability tree in such a way call for multiplication?
Let us note that if we serve a sentence, it follows that we have been convicted.
If we were given that a conviction happened and were asked to compute the probability for a sentence, the answer would be 0.7, and we are done.
Is being convicted given? No. Go up the tree.
Being convicted means we were arrested.
Is being arrested given? No. Go up the tree.
Being arrested means we were reported. Given? No. Up.
Being reported means we committed an assault. This one is given.
Oh also, note that $S = R \cap A \cap C \cap S$, that is the event S is equal to the events R, A, C and S all happening together since there is no way someone can be sentenced if they are not first convicted, arrested, reported and are guilty of assault.
Recall we noted earlier: It seems that the only way to arrive at S from As is through R, A, C and S. This is correct as unreported assaults do not result in arrests, not being arrested cannot result in a conviction and not being convicted means not serving.
Thus, $P(S | As) = P(R \cap A \cap C \cap S | As)$.
By definition of conditional probability, we have
$P(R \cap A \cap C \cap S | As) = \frac{P(R \cap A \cap C \cap S \cap As)}{P(As)}$.
If we could say that the events R, A, C, S and As are independent, then we would have $\frac{P(R \cap A \cap C \cap S \cap As)}{P(As)} = \frac{P(R)P(A)P(C)P(S)P(As)}{P(As)}$.
Unfortunately, they are not independent, I think. If not, there is a rule here we can use called the chain rule of probability.
We compute $P(R \cap A \cap C \cap S \cap As)$ as follows:
$P(R \cap A \cap C \cap S \cap As) = P(S | C \cap A \cap R \cap As) P(C | A \cap R \cap As) P(A | R \cap As) P(R|As) P(As)$
Hey look something we know, P(R|As) = 0.5.
What about the others?
We could use the extremely long and tedious process of doing things like:
$P(A | R \cap As) = \frac{P(A \cap R \cap As)}{P(R \cap As)}$
or we could take note of the fact that
$R \cap As = R$
$A \cap R \cap As = A$
$C \cap A \cap R \cap As = C$
This is true by similar reasoning to $S = R \cap A \cap C \cap S$.
Thus, we have
$P(R \cap A \cap C \cap S \cap As) = P(S|C) P(C|A) P(A|R) P(R|As) P(As)$
Hey wait, we don't know P(As). All we know is that it happened.
That's okay, we don't want to compute $P(R \cap A \cap C \cap S \cap As)$. We instead want to compute
$P(R \cap A \cap C \cap S | As) = \frac{P(R \cap A \cap C \cap S \cap As)}{P(As)} = \frac{P(S|C) P(C|A) P(A|R) P(R|As) P(As)}{P(As)}$.
Alternatively, you can write $P(R \cap A \cap C \cap S \cap As| As)$ and then note that $P(As | As) = 1$.
To understand chain rule of probability more, you may want to check out The Birthday Problem. It's a popular probability problem.
