1

Problem 2a here on page 882, translated

Prove the statement

If $\lambda\in \sigma(A)$, so $\lambda^p \in\sigma(A^p) \forall p\in\mathbb N.$

(where $\lambda$ is an eigen-value and $\sigma(A)$ is a set of the eigen-values)

Suppose arbitrary $A$ so that $\lambda\in\sigma(A)$. By the definition of eigen-value, we have a non-zero $\bar{x}$ so that $A\bar{x}=\lambda \bar{x}$ where $\bar{x}\in\mathbb R^n$, $\lambda\in\mathbb R$ and $A$ is some matrix such that $A\in R^{n\times m}$.

Diversion I earlier abserved here, $A\bar{x_1}=\lambda_1\bar{x_1}$ so $A^2\bar{x_1}=\lambda_1^2\bar{x_1}$ so $A^k\bar{x_k}=\lambda_k^k\bar{x_k}$ so $\lambda_k\in \sigma(A^k) \forall k\in \mathbb N$.

Now I think I must somehow use that, thinking (sorry about bad quality but it is only meant for a very fast draft) -- basically the junk means use indunction after quantifying the terms and prove with direct proof.

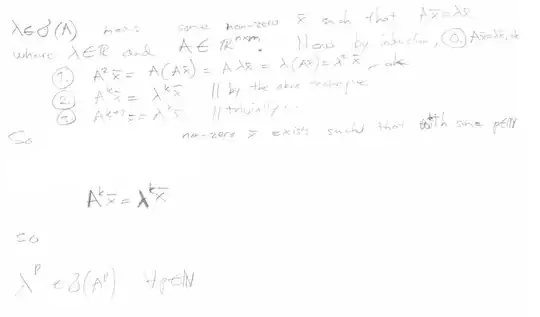
enter image description here

Goal We need to prove that $\forall p\in\mathbb N : \exists \bar{x}\in\mathbb R \not =\bar{0} : A^p \bar{x}=\lambda^p\bar{x}$.

Community
  • 1
hhh
  • 5,469
  • 3
    The "trivial solution candidate" seems like a pointless waste of time. You were not asked to find an $A$ such that the result holds for that $A$. You were asked to show the result holds for all $A$. Finding an $A$ for which the result holds makes essentially no progress towards the required proof. – André Nicolas Apr 04 '12 at 21:00
  • 1
    What do you mean, "vacuous"? (The premise is not false; and we are not quantifying over the empty set, so I do not understand what it is you mean by 'vacuous'). If you mean "easy", yes, this is not a hard problem. Also: $\lambda_1$, $\lambda_k$, $x_1$, $x_k$ have no intrinsic meanings; you must specify what $x_1$ is; $\lambda_1$ and $\lambda_k$ should just be $\lambda$. Note that having a vector $x$ such that $Bx=\mu x$ does not, by itself, show that $\mu\in\sigma(B)$; you also need $x\neq 0$. – Arturo Magidin Apr 04 '12 at 21:38
  • @ArturoMagidin: I know by now -- but I tried to not change the question so your answer is still valid... – hhh Apr 04 '12 at 21:39
  • @hhh: Well, that's nice of you, but I can edit my answers with the best of them (and faster than many). (-; – Arturo Magidin Apr 04 '12 at 21:40
  • 2
    Your goal is not quite right: you want to prove that $\forall p\in\mathbb{N}$ there exists $\overline{x}$ such that $A^p\overline{x}=\lambda^p\overline{x}$. (The $\overline{x}$ does not have to be the same for every $p$, although as it happens it can be; but, from a logical standpoint, this is not required). See this question for the difference between "there exists $\overline{x}$... for all $p$" and "for all $p$, there exists $\overline{x}$". – Arturo Magidin Apr 04 '12 at 21:54
  • It would be better to replace your 1, 2, and 3 by an actual proof by induction on $k$ (which is essentially what you are doing, but justifying it with hand-waving). Also, $\overline{x}$ is not in $\mathbb{R}$, and if you write $\overline{x}\in\mathbb{R}\neq 0$, then you are asserting that $\mathbb{R}$ is not zero, which is not what you mean. – Arturo Magidin Apr 05 '12 at 04:09
  • The solution given was like the draft in the above, perhaps I was just overengineering. – hhh Apr 15 '12 at 19:20

1 Answers1

1

I don't understand why you would consider the identity matrix separately. There is absolutely no reason to do so.

(In addition, it is very bad form to begin a proof for a statement that has an implied universal quantifier (here, "for every matrix $A$") by saying "Let's choose...". One cannot prove a universal statement by choosing a particular instance (unless the universe has one and only one element, in which case you aren't really choosing anything). If you are really going to deal with the issue by cases, then it is much better phrasing to begin by saying "Let $A$... Then either $A=[1]$ or $A\neq [1]$; if $A=[1]$ then ... If $A\neq[1]$, then ..." or some such.)

Remember the definition of "eigenvalue". Given a square matrix $B$, a scalar $\lambda$ is an eigenvalue of $B$ if and only if there exists a nonzero vector $\mathbf{x}$ such that $B\mathbf{x}=\lambda\mathbf{x}$.

If $\lambda\in \sigma(A)$, then that means that there exists a nonzero vector $\mathbf{v}$ such that $A\mathbf{v}=\lambda\mathbf{v}$.

In order to show that $\lambda^p\in\sigma(A^p)$, you need to show that there exists a nonzero vector $\mathbf{x}$ such that $A^p\mathbf{x}=\lambda^p\mathbf{x}$. The observation you make tells you which vector $\mathbf{x}$ you might want to select, and how to show that you do, in fact, get the desired equality.

If such a vector exists, then you are done: you've proven that if $\lambda\in\sigma(A)$, then necessarily $\lambda^p\in\sigma(A^p)$.

Your solution to the general case is poorly presented: you never specify that $\mathbf{x}_1\neq\mathbf{0}$, and a $\mathbf{x}_k$ appears ex nihilo in the final clause. What is $\mathbf{x}_k$?

Arturo Magidin
  • 398,050
  • 2
    @hhh: I agree wholeheartedly with Andre Nicolas's comment above. Whatever you want to start with in your scratch work is fine, but it is a waste of space and confusing to include it in your final proof. It's just very bad form to begin the proof by essentially saying "Let's choose $A$ to be ..." It's like beginning a proof that every positive integer is greater than $0$ by saying: "Let's pick $n$ to be 100. Then it's bigger than $0$, and we're fine." Even if you will eventually get around to proving it in general, it gives the wrong impression to the reader. – Arturo Magidin Apr 04 '12 at 21:02
  • @hhh: Also, there is a qualitative difference between making a problem "a bit less hard" as a first step, and going all the way to taking the trivial case. Considering $8$ and expressing it as $5+3$ is not really a good way to start trying to prove Goldbach's conjecture... – Arturo Magidin Apr 04 '12 at 21:21
  • 2
    @hhh: I'm not trying to patronize you, I'm trying to explain why, even if you find it helpful to do on your own, it is not a good thing to include in your write-up; it's confusing to the reader, and it will suggest to a grader/reader that you do not understand the logic of the proof (even if you do); and I am also trying to explain that what Tao is suggesting is not what you are doing, so invoking him as authority for you doing it suggests you did not understand his point (which is a good one in general). I don't see where I said anything about "hiding stuff". – Arturo Magidin Apr 04 '12 at 21:33
  • 1
    @hhh: If you want to say that you are considering special cases for the purpose of seeing how the result would apply to those specific/special cases, then I would suggest phrasing it so explicitly: saying "For instance, in the case of $A=[1]$, this would mean..." rather than saying "Let's choose $A$..." The latter phrasing is the typical phrasing one uses when trying to establish that there exists an $A$ with the property (which is why it is confusing to have it when trying to prove that for every A, $A$ will have the property). – Arturo Magidin Apr 04 '12 at 21:35
  • Sure you are right but I was trying to explain my philosophy: if stuck, try simpler -- perhaps then you see the point of the q. Please, clarify this discussion about trivial case, it is red-herring clearly. I removed it...a bit hard to concentrate with this trivial mess here. – hhh Apr 04 '12 at 21:36