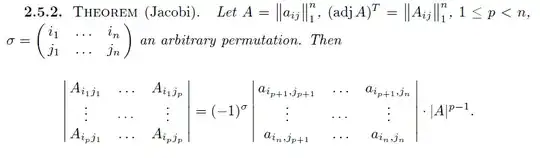3

It is by definition that entries of the adjugate matrix $\text{adj}(A)$ are the corresponding $(n-1)$-minors of $A$ (up to a sign). What can we say about the $k$-minor of $\text{adj}(A)$ in relation to minors of $A$?

I have tried some cases starting from the definition of determinant (just like the proof of the Laplace expansion), but so far no luck. But I guess it is some kind of complementary minor in $A$.

Troy Woo
  • 3,579

1 Answers1

4

Never mind...I find this Jacobi's theorem from Prasolov's (yes...every time...) book Problems and theorems in linear algebra: enter image description here

General case follows immediately from permutating the rows and columns.

darij grinberg
  • 17,777
Troy Woo
  • 3,579
  • Would you mind clarifying what $(-1)^{\sigma}$ means? I am confused because $\sigma$ is a matrix. – mzp Apr 20 '16 at 14:37
  • @mzp It is simply the signature of the permutation $\sigma$. $\sigma$ is not a matrix...Go read Prasolov's Problems and theorems in linear algebra. – Troy Woo Apr 20 '16 at 22:52