8

Let $G$ be a group of order $5$ with elements $a, b, c, d, 1$ where $1$ is the identity element. This is the definition of the group.

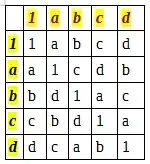
enter image description here

We all know that this can't be a group because any group of order $5$ is abelian but according to my definition this group is not abelian. But my question is why can't this be a group when it satisfies all the criteria mentioned in the definition of a group.

I wish to find a reason for its ability of not being a group just from the definition of group. For example one can say that the diagonal elements are $1$, which means we have subgroups of order $2$, which is not possible for a group of order $5$. But this is not what I am seeking. Please explain me using nothing more than just the four criteria of the definition of group.

Ken
  • 3,751
Mix
  • 267
  • 1
    Is there any quicker way of checking associativity right from the table? I am asking because suppose I have a table which is actually associative then how do I prove it? By testing each? – Mix May 13 '15 at 13:38
  • 1
    As far as I know, there is not as yet a method of checking associativity by table inspection. :( – Ken May 13 '15 at 13:48
  • 1
    While for example "commutativity" translates to a nice visual property of the table, "associativity" does not, unfortunately. – azimut May 13 '15 at 13:58
  • 4
    Given an $n \times n$ multiplication table, associativity can be checked in time $O(n^2 \log n)$, which is better than the naive $O(n^3)$, and you clearly can't do better than $O(n^2)$. But, apparently, if you choose three elements randomly in a non-associative table, then the probability that this triple will fail the test is at least $1/8$, so in practice you can expect to detect non-assiciativity quickly. See https://rjlipton.wordpress.com/2010/06/03/an-amplification-trick-and-stoc-2010/ – Derek Holt May 13 '15 at 14:00
  • 1
    Relevant: Is there an easy way to see associativity or non-associativity from an operation's table? – MJD May 13 '15 at 14:53

4 Answers4

7

You see that it's an operational system, has a neutral element, and is invertible straight from the table, so the only thing left to check is associativity.

Here, we have $(aa)c = 1c = c \neq b = ad = a(ac)$.

(The good news is that, if an operational system isn't associative, it usually doesn't take too long to find a counterexample.)

Ken
  • 3,751
  • Actually I was working with that problem of Herstein which says-- prove that a group of order 5 is abelian. What I did is I took up case by case and showed that in each case they are abelian. But in a particular case the above table popped up, and that is why I asked this question. But after getting answers to it I realized that I was ignoring the associativity part in all the cases. So now I have to check (in each case) the associativity. And therefore I asked for a quicker way of doing that. Anyways thanks a lot for your help. – Mix May 13 '15 at 13:59
  • Sneaky authors! But I understand your question better now. You're welcome. :) – Ken May 13 '15 at 14:02
3

$$(a\cdot b)\cdot b= c\cdot b= d \neq a=a\cdot 1=a\cdot (b\cdot b)$$

Daniel
  • 6,999
3

It's not associative: The least exciting of the properties you have to check.

$(ca)d = bd = c$, but $c(ad) = cb = d$

Zach L.
  • 6,633
2

$$(ab)d=a \neq d= a(bd)$$

Associativity fails.

N. S.
  • 132,525