Calculating $\int_{0}^{\infty}\sin(x^{2})dx$

Question

I am supposed, in an exercise, to calculate the above integral by integrating $f(z) = e^{-z^{2}}$ on the following countor: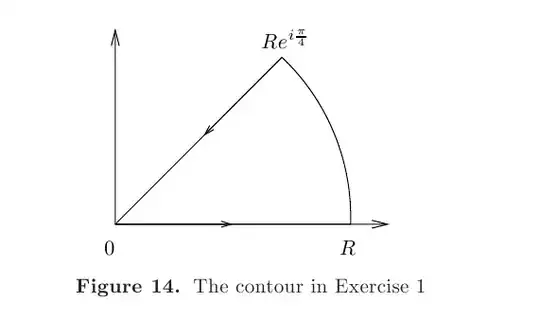

I began by separating the path $\gamma$ into three paths (obvious from the picture), and parametrizing each as follows:

$\gamma_{1} : [0, R] \rightarrow \mathbb{C}$ with $\gamma_{1}(t) = t$

$\gamma_{2} : [0, \frac{\pi}{4}] \rightarrow \mathbb{C}$ with $\gamma_{2}(t) = Re^{it}$

$\gamma_{3} : [0, \frac{\sqrt{2}R}{2}] \rightarrow \mathbb{C}$ with $\gamma_{3}^{-}(t) = t + it$ (with reverse orientation).

Then we can say that $\displaystyle\int_{\gamma} f(z) dz = \displaystyle\int_{\gamma_{1}} f(z) dz + \displaystyle\int_{\gamma_{2}} f(z) dz - \displaystyle\int_{\gamma_{3}^{-}} f(z) dz = 0$ since the path is closed.

Now $\displaystyle\int_{\gamma_{1}} f(z) dz = \displaystyle\int\limits_{0}^{R} e^{-t^{2}} dt$. We also get $\displaystyle\int_{\gamma_{3}^{-}} f(z) dz = -(i + 1) \displaystyle\int\limits_{0}^{\frac{\sqrt{2}R}{2}}e^{-2it^{2}} dt$. After playing around with sine and cosine a bunch to evaluate that last integral, I get:

$$0 = \int\limits_{0}^{R} e^{-t^{2}} dt + \int\limits_{\gamma_{2}} f(z) dz - \frac{i + 1}{\sqrt{2}} \int\limits_{0}^{R} \cos(u^{2}) du + \frac{i - 1}{\sqrt{2}} \int\limits_{0}^{R} \sin(u^{2}) du$$

I could not evaluate the integral along the second path, but I thought it might tend to 0 as $R \rightarrow \infty$. Then taking limits and equating real parts we get

$$\frac{\sqrt{2 \pi}}{2} = \displaystyle\int\limits_{0}^{\infty} \sin(u^{2}) du + \displaystyle\int\limits_{0}^{\infty} \cos(u^{2}) du$$

If I could argue that the integrals are equal, I would have my result.. But how do I?

So I need to justify two things: why the integral along $\gamma_{2}$ tends to zero and why are the last two integrals equal.

Answer 1

Your parametrisation of the third integral is rather complicated. Why not just write $\gamma_3:[0,R]\rightarrow \mathbb{C}$, $t\mapsto -e^{\pi i/4}t$. Then the integral becomes $$ \int_R^0 e^{-e^{\pi i/2}t^2}e^{\pi i/4}dt = \int_R^0 e^{-it^2}e^{\pi i/4}dt = e^{\pi i/4} \int_R^0 \cos t^2 - i \sin t^2 dt. $$ I am sure you can take it from there.

As for bounding the integral $\int_{\gamma_2}e^{-z^2}dz$, the length of the contour grows linearly with $R$. How fast does the maximum of the integrand decay? It's the standard approach, using the fact that $$ \left|\int_\gamma f(z) dz\right|\leq \sup\{|f(z)|: z \in \text{ image of }\gamma\}\cdot \text{length of }\gamma. $$

Answer 2

$$\int_0^R e^{-t^2}dt= \frac{\sqrt{\pi}}{2}+o(1). \tag{1}$$

$$t\in\left[0,\frac{\pi}{4}\right] \implies \operatorname{Re}(Re^{it})\ge \frac{R}{\sqrt{2}} \implies \left|\int_{\gamma_2}e^{-z^2}dz\right|\le R\frac{\pi}{4}e^{-R^{\,2}/2}\to0 \tag{2}$$

$$\alpha=\int_0^M e^{it^2}dt \implies \int_0^M \sin(t^2)dt=\frac{\alpha+\overline{\alpha}}{2}. \tag{3}$$

Try using these deductions for $\gamma_1$, $\gamma_2$ and $\gamma_3$ respectively.

Answer 3

An easy way to evaluate $\int_{0}^{\infty}\sin(x^{2})dx$

$$\int_0^{\infty}e^{-ax^2}dx=\frac{\sqrt{\pi}}{2\sqrt{a}}$$ Now replace $a\rightarrow ia$

$$ \int\limits_0^\infty \cos \left( {a{x^2}}\right)dx-i \int\limits_0^\infty \sin \left( {a{x^2}}\right)dx= \frac{\sqrt{\pi}}{2\sqrt{a}\sqrt{i}} $$ But

$$\frac{1}{\sqrt{i}}= \frac{1}{\sqrt{2}}-\frac{i}{\sqrt{2}} $$ So

$$ \int\limits_0^\infty \cos \left( {a{x^2}}\right)dx=\int\limits_0^\infty \sin \left( {a{x^2}}\right)dx= \frac{\sqrt{\pi}}{2\sqrt{2a}} $$