If $\gcd(a,b)=d$, then $\gcd(a/d, b/d)=1$

Question

So, I think that I understand the proof.

The idea is that we want to establish the inequality that says that $c\leq 1$ and with the idea that the $\gcd$ of two numbers is always greater or equal than $1$, then we will know that can't be negative or zero, thus $c=1$ (correct me if my understanding isn't correct).

The idea of how I understand a proof is that we must say only what is necessary, any excess verbose is bad. So, the part of the proof that I find weird it's when it says: "We will do this by showing that $c\leq 1$ and $c\geq 1$." Where did the author prove that the inequality $c\geq1$? Is there something that I'm missing?

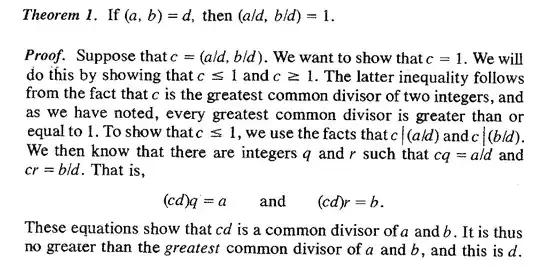
enter image description here

Thus $cd \leq d$. Since $d$ is positive, this gives $c \leq 1$. Hence $c = 1$, as was to be proved.

Thank you for the reference, I appreciate it. I just wanted to understand this one. What do you think of the proof ? — , May 12 '15 at 03:29
See also: Proving $\gcd \left(\frac{a}{\gcd (a,b)},\frac{b}{\gcd (a,b)}\right)=1$ and Proving that $\gcd\left(\frac a {\gcd(a,b)},\frac b {\gcd(a,b)}\right) =1$. — Martin Sleziak, Jul 05 '20 at 13:43

score 3 · Accepted Answer · answered May 12 '15 at 02:31

3

$c \ge 1$ is proved starting with the sentence

The latter inequality follows from ..

answered May 12 '15 at 02:31

mvw

34,562

oh, It was that simple... I thought there was gonna be a sort of construction... thank you then! – May 12 '15 at 02:36
Yes, there was the 5 min that I had to wait – May 12 '15 at 02:43

If $\gcd(a,b)=d$, then $\gcd(a/d, b/d)=1$

1 Answers1

Linked