Angle between 2 points

Question

Given the following image:

$\hskip{1.5 in}$ 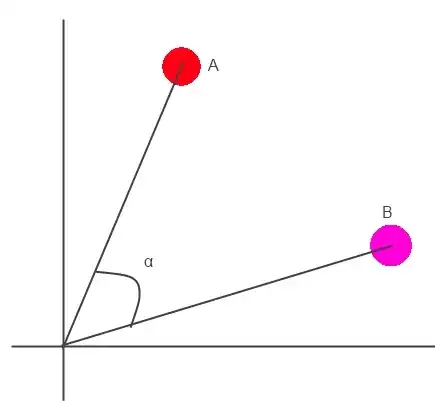enter image description here

Supposing $A(100, 300)$ and $B(300, 100)$, how can I find the angle $\alpha$ between A and B?

On a side note, what's the main difference between a point and a vector? translating a point to a vector is as simple as Point = Vector? Sometimes I find articles where the terms are interchangable

Your image shows that you are asking for the angle at the origin — Henry, Apr 03 '12 at 20:49
ok, how should I edit my main question in order to describe that I want to know angle alpha? Thank you :) — aljndrrr, Apr 03 '12 at 20:52

score 5 · Accepted Answer · answered Apr 03 '12 at 20:53

5

Hint: You may have been taught about the dot product, perhaps something like $$\mathbf{a} \cdot \mathbf{b}=\left\|\mathbf{a}\right\| \, \left\|\mathbf{b}\right\| \cos \theta$$ so how might you apply that here?

answered Apr 03 '12 at 20:53

Henry

157,058

so it's $\theta = \arccos((\mathbf{a} \cdot \mathbf{b})/(\left|\mathbf{a}\right| , \left|\mathbf{b}\right|))$ ? – aljndrrr Apr 03 '12 at 22:09
1

Yes (though you might want to take care about the sign) – Henry Apr 03 '12 at 22:18
Coming from a google search, this answer being a "hint" and not an actual answer to the question is frustrating. – FMaz008 Feb 14 '23 at 16:38

score 4 · Answer 2 · answered Apr 03 '12 at 20:57

4

The Atan2 function in most computer languages will take the coordinates of a point and give the angle from the origin to that point. If you take Atan2$(B_x,B_y)-$Atan2$(A_x,A_y)$ you will have it, to within multiples of $2\pi$. If you use the usual arctangent you need to worry about which quadrant you are in.

Points are exactly that, locations in the plane (in 2D). Vectors are things with a length and a direction. You can make a correspondence between a point and the vector from the origin to that point, which seems to be what you are doing. But a vector can also be from (1,2) to (4,8), for example. This vector has coordinates (3,7).

answered Apr 03 '12 at 20:57

Ross Millikan

374,822

Not sure I'm understanding something. Where I have p1.x = -384, p1.y = 0, p2.x = -192, and p2.y=-332.5537 and doing A = WorksheetFunction.Atan2(P2.x, P2.y) - WorksheetFunction.Atan2(P1.x, P1.y), My A value is -5,2360... A * 2 * 3.1416 is -32,89... I know for a fact the angle is 60 degrees. I'm no where near that if I take the radiant result and convert it to degrees ( A * 180# / PI ). – FMaz008 Feb 14 '23 at 17:13
This formula seems to work better: https://math.stackexchange.com/a/855541/1146278 – FMaz008 Feb 14 '23 at 17:27

score 2 · Answer 3 · answered Apr 03 '12 at 20:53

Let $A={A_x \choose A_y}$. Then you subtract the angle $\angle A$ (between $A$ and the $x$-axis) from $\angle B$ (the angle between $B$ and the $x$-axis).

Use the inverse of $\tan(\angle A)=\frac{A_y}{A_x}$ to get $\alpha= \tan^{-1}(\frac{A_y}{A_x})-\tan^{-1}(\frac{B_y}{B_x})$.

Angle between 2 points

3 Answers3

Linked

Related