2

So the question I have is

Let S be a non-negative random variable. By writing the probability as an expectation and using Fubini's theorm, show that

$ES^4=\int_0^\infty4t^3P(S>t)dt$

so I found on wikipedia http://en.wikipedia.org/wiki/Expected_value#General_definition

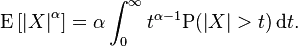
enter image description here

but it does not show how to prove it.

My attempt is somehow using the chain rule but i don't know how do you change S into t.

Did
  • 279,727
Yau Kin Hoe
  • 299

2 Answers2

4

Hint: Note that for $X$ non negative random variable, and $x>0$ and $\alpha > 1$

  1. $$x^\alpha = \int_0^x\alpha u^{\alpha-1}du$$
  2. $$E[X^\alpha] = \int_0^\infty x^\alpha dF(x)= \int_0^\infty \int_0^x\alpha u^{\alpha-1}du dF(x)$$ $$ = \int_0^\infty \int_0^\infty\alpha u^{\alpha-1}1_{\{u \leq x\}}du dF(x)$$

Swap the integrals using Fubini Tonelli theorem, get rid of the indicator function and you will have your result. Try the steps for yourself and let me know if you have problems.

Gautam Shenoy
  • 10,318
  • then $$\int_0^\infty1_{{u \leq x}}dF(x) = 1-F(u\leq x)=P(u>x)$$ ? – Yau Kin Hoe May 11 '15 at 13:20
  • 1
    No. It evaluates to $\int_0^\infty 1_{{u\leq x}} dF(x) = \int_u^\infty dF(x) = P[X > u]$ – Gautam Shenoy May 11 '15 at 13:23
  • Another way to understand this is to see that it is same as $E[1_{{u \leq X}}] = P[X > u]$ – Gautam Shenoy May 11 '15 at 13:27
  • So my answer now would be using the symbols above would be $$E[S^4] \ = \int_0^{\infty} S^4 dP \ = \int_0^{\infty} \int_0^{\infty} 4t^3 1_{s>t} dtdP \ =\mbox{Fubini} \int_0^{\infty} \int_0^{\infty} 4t^3 1_{s>t} dPdt \ = \int_0^{\infty} 4t^3 \int_t^{\infty} dPdt \ = \int_0^{\infty} 4t^3 P(S>t) dt$$ – Yau Kin Hoe May 11 '15 at 13:32
  • 1
    Yes it is. Steps are all correct. – Gautam Shenoy May 11 '15 at 13:34
  • amazing thank you Gautam ! – Yau Kin Hoe May 11 '15 at 13:39
  • 1
    Actually there is serious mistake in the very first step, which should read $$E(S^4)=\int_\Omega S^4dP.$$ Note that this first step is unnecessary, one can do all that follows keeping the form $E(\cdots)$. – Did May 11 '15 at 15:54
0

I'm typing this on my phone so I hope there won't be that many typos.

If you assume that your random variable is nice enough, then it has a density function $f (t)$ and a distribution function $F(t) = P ( X \leq t)$ such that $$\frac {d}{dt} (1 - F) = -f$$

In this case you can compute \begin{align*} E [X] &= \int X dP = \int t^{\alpha} dP_X = \int t^{\alpha} \cdot f (t) dt \\ & = - \int t^{\alpha} (1-F)'(t) dt = -[t^{\alpha}(1-F(t))]_{t=0}^{\infty} + \int \alpha t^{\alpha - 1} (1-F(t)) dt \\ & = \alpha \int t^{\alpha-1} P (X > t ) dt \end{align*}

j4GGy
  • 3,721