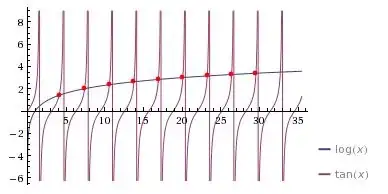
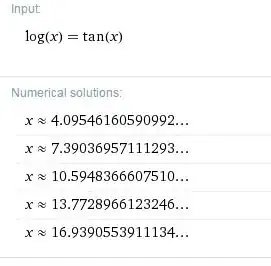
In each interval $\left(\pi n - \frac{\pi}{2}, \pi n + \frac{\pi}{2}\right)$ there is exactly one solution $x_n$ (i.e. $\tan x_n = \ln x_n$), and, when $n$ is large, it appears that $x_n$ is approximately $\pi n + \frac{\pi}{2}$. Let's show this.
Since $\tan$ is $\pi$-periodic we have
$$\tan\left(\pi n + \frac{\pi}{2} - x_n\right) = \tan\left(\frac{\pi}{2} - x_n\right)$$
$$\hspace{2.4 cm} = \frac{1}{\tan x_n}$$
$$\hspace{2.6 cm} = \frac{1}{\ln x_n} \to 0$$
as $n \to \infty$, where the second-to-last equality follows from the identites $$\sin\left(\frac{\pi}{2} - \theta\right) = \cos \theta,$$ $$\cos\left(\frac{\pi}{2} - \theta\right) = \sin \theta.$$
Since $-\frac{\pi}{2} < \pi n + \frac{\pi}{2} - x_n < \frac{\pi}{2}$ and since $\tan$ is continuous in this interval we have $\pi n + \frac{\pi}{2} - x_n \to 0$ as $n \to \infty$.
So, we know that
$$
x_n = \pi n + \frac{\pi}{2} + o(1).
$$
Let's get an estimate for the error term. If we set $w_n = \left(\pi n + \frac{\pi}{2}\right)^{-1}$ and $z_n = w_n^{-1} - x_n$ then
$$
\tan x_n = \frac{1}{\tan z_n}
$$
by the above calculation and
$$
\ln x_n = \ln w_n^{-1} + \ln(1+w_n z_n),
$$
so the equation $\tan x_n = \ln x_n$ becomes
$$
\frac{1}{\tan z_n} = \ln w_n^{-1} + \ln(1+w_n z_n). \tag{$*$}
$$
Now $w_n,z_n \to 0$ as $n \to \infty$, so
$$
\frac{1}{\tan z_n} \sim \frac{1}{z_n}
$$
and
$$
\ln w_n^{-1} + \ln(1+w_n z_n) \sim \ln w_n^{-1}
$$
as $n \to \infty$. Thus, from $(*)$,
$$
\frac{1}{z_n} \sim \ln w_n^{-1},
$$
or
$$
z_n \sim \frac{1}{\ln w_n^{-1}} = \frac{1}{\ln(\pi n + \pi/2)}.
$$
By definition of $z_n$ we therefore get the asymptotic
$$
x_n = \pi n + \frac{\pi}{2} - \frac{1}{\ln(\pi n + \pi/2)} + o\left(\frac{1}{\ln n}\right).
$$