Limit of the series $\sum_{n=1}^{\infty}{\frac{n}{2^n}}$

Question

Can someone help me to find the sum?

$$\sum_{n=1}^{\infty}{\frac{n}{2^n}}$$

Thanks for the link @DavidMitra. I could now delete my answer without any loss to the site, but my picture is different. Making it CW instead. — Jyrki Lahtonen, May 09 '15 at 13:49
This specific sum has been handled for example here. The one linked to by David is older, and more general. Closing this as a duplicate. — Jyrki Lahtonen, May 09 '15 at 14:05

score 5 · Answer 1 · answered May 09 '15 at 13:27

5

First observe that $\sum_{n=0}^\infty x^n=\frac1{1-x}$ for $|x|<1$ and then differentiation and letting $x=1/2$ gives the answer...

answered May 09 '15 at 13:27

k1.M

5,428

score 1 · Accepted Answer · answered May 09 '15 at 14:02

Let \begin{align} S &= 1\cdot \frac{1}{2} + &2 \cdot \frac{1}{2^2} + 3 \cdot \frac{1}{2^3} + \cdots\\ \frac{1}{2}S &= &1 \cdot \frac{1}{2^2} + 2 \cdot \frac{1}{2^3} + \cdots \end{align}

then we can get \begin{align} \frac{1}{2}S &= 1\cdot \frac{1}{2} + 1 \cdot \frac{1}{2^2} + 1 \cdot \frac{1}{2^3} + \cdots\\ &= \sum_{n=1}^{\infty} \frac{1}{2^n}=1 \end{align}

so $S = 2$.

score 0 · Answer 3 · answered May 09 '15 at 13:47

0

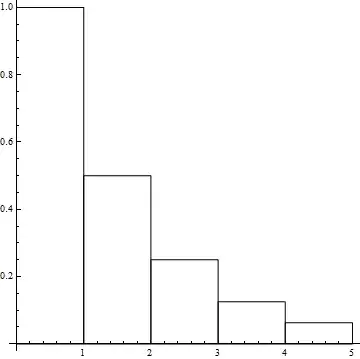
Split the same region to infinitely many rectangles in two different ways. The red way gives the area as the sum in question. The black way is something even easier to calculate.

enter image description here

answered May 09 '15 at 13:47

Jyrki Lahtonen

133,153

Limit of the series $\sum_{n=1}^{\infty}{\frac{n}{2^n}}$

3 Answers3