Let $x_1 = a, x_{n+1} = \sqrt{5 + x_n}$. Then
A. there exists $a \geq 0 $ such that sequence $x_n$ is unbounded.
B. for any $a \geq 0 $ sequence has a limit
The answer is supposed to be B, but I believe that it's wrong, i.e. the correct answer is A. The easiest way to see this is to look on the figure of intersection of $y=x$ and $y = \sqrt{5+x}$. Start at any point to the right of the intersection, and you'll go to infinity.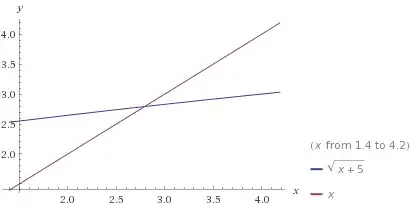
My question: am I right, or did I miss something?
The correct answer is B, sorry.
If we take $a$ to the right of the intersection, we will coverge to the intersection. For example taking $a=1000$, we have $x_2\approx31.7$ and $x_3\approx6.06$ and $x_4\approx3.33$.
Let $\xi (u) =\sqrt{u+5}$ then $\xi :\left< 0 ,\infty\right) \to \left< 0 ,\infty\right) $ and $\xi ' (u) =\frac{1}{2\sqrt{u+5}}\leqslant \frac{1}{2}$ hene it is a contraction in the complete metric space $\left<\left< 0 ,\infty \right) , |\cdot |\right>$ so by Banach Fixed Point Theorem for all $a\in \left< 0 ,\infty\right)$ the sequence defined $x_0 =a , x_{n+1} =\xi (x_n )$ is convergent to unique fixed point of $\xi$ which is equal to $2^{-1}\cdot (1+\sqrt{21} ).$