2

I have two dimensional Cartesian system and I need to check if certain point is within the geometry formed by four other points. I have few thousands different geometries all with different points to check. So I'm writing a program for it.

HERE is a solution method I started with and it works if the data points are always given in same order: A(x,y) B(x,y) C(x,y) and D(x,y) with the point P(x,y). (But it's not)

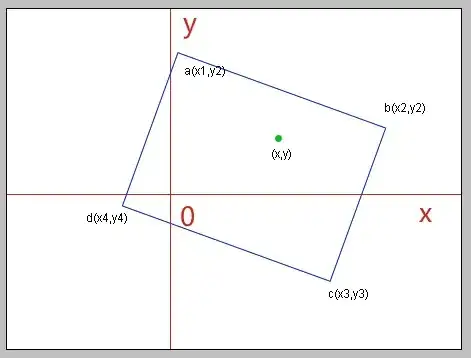
Cartesian Coordinates: (Image taken from above link)

My points are randomly given, so when connecting between the dots they might go to "opposite" corner so the drawing wouldn't be box exactly.

Case 1: A(x,y) B(x,y) C(x,y) D(x,y) with the point P(x,y).
Case 2: C(x,y) A(x,y) D(x,y) B(x,y) with the point P(x,y).
Case 3: D(x,y) B(x,y) A(x,y) C(x,y) with the point P(x,y).
Case 4: B(x,y) D(x,y) A(x,y) C(x,y) with the point P(x,y).

So it's impossible to write a program with earlier mentioned method. I've been looking around and I can't seem to find a method that doesn't care in which order it gets the coordinates of the geometry.

Thanks.

Community
  • 1
Bjartmar
  • 123
  • You are going to have a problem if your shape is concave ("arrowhead" or "dart") because there may be more than one way to draw a quadrilateral with those vertices. Consider A(0,0), B(0,5), C(3,3), D(1,3). – tomi May 07 '15 at 22:59
  • All of my data would make a some kind of a "box" as it's a generated data from a camera detecting that kind of shape. But for some unresolvable reason it doesn't mark the corners in same order. So I shouldn't get an arrowhead or a dart. – Bjartmar May 08 '15 at 09:52
  • If the 4 pts always form a rectangle as in the diagram then you can use the "dot product" to find lines that form a right-angle. E.g. Focus on pt A. If $AD\cdot AC=0$ then A's neighboring points are C,D and the rectangle is ACBD. If not 0, next if $AD\cdot AB=0$ then A's neighboring points are B,D and the rectangle is ABCD. If that's not 0 either, if $AC\cdot AB=0$ then A's neighboring points are B,C and the rectangle is ABDC. Exactly 1 of these 3 results must be 0. Once you find this, use the method you refer to to test P. Dot Product defn: $AD\cdot AC=(x_4-x_1)(x_3-x_1)+(y_4-y_1)(y_3-y_1)$. – Mick A May 08 '15 at 14:28
  • Thanks for the comment but unfortunately I do not always have right-angles. – Bjartmar May 08 '15 at 15:32
  • So what we know is that the 4 points form a convex quadrilateral? – Mick A May 08 '15 at 18:58
  • Yes, that's true. But I know that non of the angles, when the correct neighbours have been found, are more than 180°... if that could help. – Bjartmar May 08 '15 at 19:16

2 Answers2

1

Consider point $A$. We need to find which two of the three points $B,C,D$ are its neighbours in the quadrilateral. So we consider the three line segments (or we can consider them as 2-dimensional vectors): $AB,AC,AD$. If $A's$ neighbours are $B,C$, say, then $\angle BAC$ will be greater than both $\angle BAD$ and $\angle CAD$, and therefore their cosines will have the opposite relationship. So we look for the angle with the small cosine.

So calculate:

\begin{eqnarray*} \cos(\angle BAC) &=& \dfrac{AB\cdot AC}{\|AB\|\|AC\|} \\ \cos(\angle BAD) &=& \dfrac{AB\cdot AD}{\|AB\|\|AD\|} \\ \cos(\angle CAD) &=& \dfrac{AC\cdot AD}{\|AC\|\|AD\|}. \end{eqnarray*}

Whichever is the least of these determines the two neighbouring points of $A$.

You can then use the method from the other question you refer to to check for point $P$.

Example: $A=(-2,1),\quad B=(2,6),\quad C=(5,2),\quad D=(1,-4)$.

\begin{eqnarray*} AB &=& (2-(-2))\;\mathbf{i} + (6-1)\;\mathbf{j} = 4\mathbf{i} + 5\mathbf{j} \\ AC &=& (5-(-2))\;\mathbf{i} + (2-1)\;\mathbf{j} = 7\mathbf{i} + \mathbf{j} \\ AD &=& (1-(-2))\;\mathbf{i} + (-4-1)\;\mathbf{j} = 3\mathbf{i} - 5\mathbf{j} \\ && \\ \|AB\| &=& \sqrt{4^2+5^2} = \sqrt{41} \\ \|AC\| &=& \sqrt{7^2+1^2} = \sqrt{50} \\ \|AD\| &=& \sqrt{3^2+5^2} = \sqrt{34} \\ && \\ AB\cdot AC &=& 4\times 7 + 5\times 1 = 33 \\ AB\cdot AD &=& 4\times 3 + 5\times (-5) = -13 \\ AC\cdot AD &=& 7\times 3 + 1\times (-5) = 16 \\ && \\ \therefore\quad \cos\angle BAC &=& \dfrac{33}{\sqrt{41}\sqrt{50}} \\ \cos\angle BAD &=& \dfrac{-13}{\sqrt{41}\sqrt{34}} \\ \cos\angle CAD &=& \dfrac{16}{\sqrt{50}\sqrt{34}}. \end{eqnarray*}

The smallest cosine is $\cos\angle BAD$ so $A$'s neighbours are $B,D$ and the quadrilateral is $ABCD$.

Mick A
  • 10,208
  • I like this answer a lot (and have upvoted it) but I am going to suggest another approach in my answer. – tomi May 09 '15 at 23:32
0

Based on @bjartmar's assertion that the quadrilateral is convex, my preferred approach would be to consider the angle between the line joining P to each of the vertices and some given reference line. If the reference line were to be the North direction, then this would be like finding the bearing of each point from P. I prefer, however, to take the positive x-axis as the reference line.

Let $\hat \theta_i = \begin{cases} \tan^{-1}\left(\frac {y_i-y}{x_i-x}\right)&\textrm{ if }x_i\neq x\\ \frac \pi 2&\textrm{ if }x_i=x \end{cases}$

The standard way of calculating $\tan^{-1}$ means that $-\frac \pi 2 <\hat\theta_i\leq \frac \pi 2$

Make the following adjustments:

Let $\theta_i = \begin{cases} \hat \theta_i + \pi&\textrm{ if }x_i< x \textrm{ and } y_i>y\\ \hat \theta_i - \pi&\textrm{ if }x_i\leq x \textrm{ and } y_i<y\\ \hat\theta_i&\textrm{ otherwise } \end{cases}$

Now we have $- \pi <\theta_i\leq \pi$.

You can then arrange your vertices in increasing order of $\theta_i$

tomi
  • 9,594
  • Hi @tomi I think this will work if $P$ is inside the quadrilateral. But not necessarily when $P$ is outside. Take my example points of $A,B,C,D$. If $P=(-6,0)$ I get an order $DCAB$. If $P=(-6,2)$ I get an order $DACB$. Neither of these are right. – Mick A May 10 '15 at 02:06