Is there any geometrical interpretation as to why matrix product is not commutative?

Question

Is there any geometrical interpretation as to why matrix product is not commutative?

Similarly, is there any geometrical interpretation of matrix product when you have matrices $A$, $B$ such that $AB=BA$?

Answer 1

Geometrically, transformations on spaces are just too flexible to permit commutativity very often.

Commutativity is really very special. Maybe it isn't surprising to make examples with sets of functions on small sets that aren't commutative, or even with groups of symmetries on regular polygons. The context you want is within linear transformations. But it is very easy to find examples even with transformations as simple as $90$ degree turns around three orthogonal axes.

Pick an orthogonal basis and two of the axes, and then do $90$ degree turns in both orders.

You can think of the group generated by these transformations as the rotation symmetries of a cube in $3$-space. You could explore this with a 6-sided die or Rubik's cube.

Answer 2

Consider a simple 2-D case.

$ A=\begin{bmatrix} 1 & 0 \\0 & 2 \end{bmatrix} $ a dilation which leaves the x component unchanged and doubles the y component

and

$ B=\begin{bmatrix} 0 & -1 \\1 & 0 \end{bmatrix}$ which rotates a vector counterclockwise by 90 degrees

if we apply both transformations to the vector $v=\begin{bmatrix} 1 \\0 \end{bmatrix}$

$Av=\begin{bmatrix} 1 \\0 \end{bmatrix}$ so $BAv=\begin{bmatrix} 0 \\1 \end{bmatrix}$

however

$Bv=\begin{bmatrix} 0 \\1 \end{bmatrix}$ so $ABv=\begin{bmatrix} 0 \\2 \end{bmatrix}$

So we see that applying the rotation first will change the effect of the dilation.

Answer 3

Matrices represents linear transformations, and linear transformations (in $n$-dimensional spaces) does not commute.

This is the simple answer and we can prove this statement simply using linearity. Here a proof in $\mathbb{R}^2$ that can be easely represented geometrically with a figure.

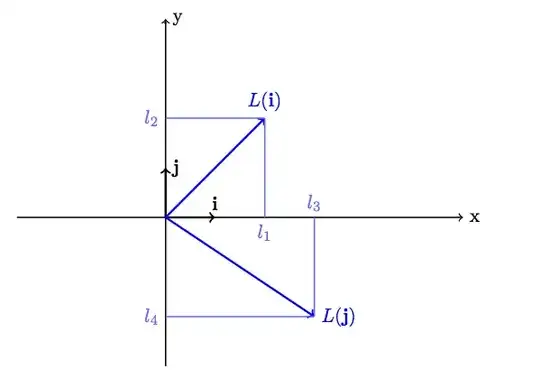
Let $\mathbf{i},\mathbf{j}$ the canonical basis and $\mathbf{v}=v_1\mathbf{i}+v_2\mathbf{j}$ a vector. By definition a linear transformation $L$ acts as: $$ L(\mathbf{v})=v_1L(\mathbf{i})+v_2L(\mathbf{j}) $$ Where $L(\mathbf{i})$ and $L(\mathbf{j})$ are vectors that we can represent as (see the figure): $$ L(\mathbf{i})=l_1\mathbf{i}+l_2\mathbf{j} \qquad L(\mathbf{j})=l_3\mathbf{i}+l_4\mathbf{j} $$

For another linear transformation $M$ we have:

$$ M(\mathbf{v})=v_1M(\mathbf{i})+v_2M(\mathbf{j}) $$ with $$ M(\mathbf{i})=m_1\mathbf{i}+m_2\mathbf{j} \qquad M(\mathbf{j})=m_3\mathbf{i}+m_4\mathbf{j} $$

Now, to show that $L$ and $M$ does not commute it is sufficient to show that $ML(\mathbf{i}) \ne LM(\mathbf{i})$. To show this fact calculate: $$ ML(\mathbf{i})=M(l_1\mathbf{i}+l_2\mathbf{j})=l_1M(\mathbf{i})+l_2M(\mathbf{j})=(l_1m_1+l_2m_3)\mathbf{i}+(l_1m_2+l_2m_4)\mathbf{j} $$ and, in the same manner, $LM(\mathbf{i})$.

You can do the same for $ML(\mathbf{j})$ and $LM(\mathbf{j})$. So you also see because a linear transformation is represented by a matrix.