10

I designed this problem and tried to solve it but didn't solve.

Choose four points $A$, $B$, $C$ and $D$ from inside of a circle uniformly and independent. What is the probability that $AC$ intersects $BD$?

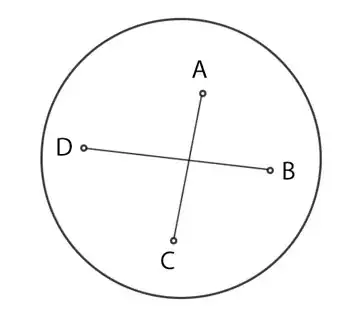
enter image description here

David G. Stork
  • 29,774
  • Even if you remove the circle, the problem would remain same. So what is the purpose of it. And according to me the probability would be infinitesimally small. – Aditya Agarwal Apr 30 '15 at 16:03
  • 1
    @AdityaAgarwal The circle constrains the locations of the points. the probability is not infinitesimally small! – David G. Stork Apr 30 '15 at 16:06
  • Using circle let us to take points uniformly from an area, and you can not take uniform points from $\mathbb{R}^2$. I think probability is near $\frac{1}{5}$. @AdityaAgarwal –  Apr 30 '15 at 16:06
  • But there is no restriction on the radius of circle.? @DavidG.Stork – Aditya Agarwal Apr 30 '15 at 16:07
  • @AdityaAgarwal Indeed, the problem is scale invariant. As such, set the circle's radius arbitrarily to $r = 1$. Alternatively, realize that for a very large circle, the range of positions where the lines can intersect increases. – David G. Stork Apr 30 '15 at 16:17

1 Answers1

3

There are 2 general cases here, either one point lies in the triangle formed by the other 3, or there is no such point. The diagram above is an example of the second case. In the first case, there is no way to connect the line points with 2 lines segments, such that the segments intersect. In the second case, it is possible, but only in the case where "opposite" points are chosen, which is 1 out of 3 possible. So, if the probability of having no point lie in the interior of the triangle formed by the other 3 is $P$, the probability is $\frac{1}{3}P$. Now the trick is how to find $P$.

[edit] As Jack notes below, this separate problem has been solved here, yielding $$P=1−\frac{35}{48 \pi^2}$$

Community
  • 1
Paul
  • 8,153
  • 3
    I agree this is the most natural approach. By this related question, http://math.stackexchange.com/questions/1243160/expected-area-of-triangle-formed-by-three-random-points-inside-unit-circle, we should have $$ P =1-\frac{35}{48\pi^2}. $$ – Jack D'Aurizio Apr 30 '15 at 15:54
  • @Paul. I have an advice: Please remove your idea that has been written as an answer, and write it as a comment behind the main post. –  Apr 30 '15 at 16:14
  • @mathstudent, first, it is too long to be a comment, and second, as a partial answer it maks more sense to be here. And with Jack's comment below the answer, everything you need is here. – Paul Apr 30 '15 at 16:50
  • @Paul Aha! I was thinking that the jacks comment does not complete the solution, but when I read it again now I found that the solution is completed. Thanks a lot. –  Apr 30 '15 at 16:56
  • @Paul if you like, you can edit your answer and write a text behind it to refer to Jacks solution. –  Apr 30 '15 at 16:58
  • The question linked in the comments shows that the probability that one particular point is in the triangle formed by the other three is $35/(48\pi^2)$. Since there are four possibilities for that point, shouldn't we instead have $P=1-\frac{35}{12\pi^2}$? – Julian Rosen Mar 23 '17 at 22:38