In addition to Rammus' answer there are less trigonometric and more concise ways of solving the problem. I will show below three methodologies: with limits, with a modification of Riemann Sums (notice that the question asks for a sumation), and finally how to express the same modified Riemann Sum as an integral.
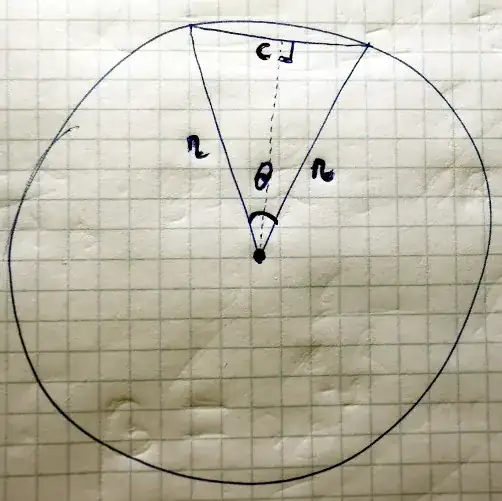
First to the intuition. You can approximate the area of the circle by dividing it into isosceles triangles.

Source: http://www.amsi.org.au/teacher_modules/the_circle.html
Notice the gap between the base of the triangles and the arc of the circle. That is the error in our approximation. By increasing the number of triangles, that region decreases. So if we increase our (n) number of triangles to infinity, the error disappears, and the base of a given triangle is equal to the arclength of a given segment.
(1) Note the equation for the area of an isosceles triangle and the equation for circumference of a circle:
$$A_{triangle} = \frac 12 \times base \times height
\\ C = 2 \pi r$$
When $n = \infty$:
$$height = r, \space base = \frac {2\pi r} n$$
Since we have $n$ triangles the total area can be expressed like this:
$$A_{circ} = \lim \limits_{n \rightarrow \infty} n \space (A_{triangle})
= \lim \limits_{n \rightarrow \infty} n \space \frac 12 \frac {2\pi r} n r$$
The n's cancel and so do the 2's, giving us: $A_{circ} = \pi r^2$
(2) Though, let's take this a step farther and see if we can rearrange this into something resembling a Reimann Sum, which works by summing infinitely many rectangles under a given function $f(x)$. It's form is:
$$
A = \lim \limits_{n \rightarrow \infty} \sum_{i=1}^{n} f(x_{i-1}) \Delta x
\\ \Delta x = \frac {b-a} n
$$
In effect $\Delta x$ is the base of the rectangle, and $f(x)$ is the height. If we want to make it a triangle we insert $\frac 12$:
$$A = \lim \limits_{n \rightarrow \infty} \sum_{i=1}^{n} \frac 12 f(x_{i-1}) \Delta x$$
Since, we are summing triangles along the circumference, $b-a = 2 \pi r - 0$ and $\Delta x = \frac {2\pi r} n$. We can also conclude that $f(x)$ is a constant function equal to $\pi$, and we will need to insert to constant $\frac 1 2$.
$$A = \lim \limits_{n \rightarrow \infty} \sum_{i=1}^{n} \frac 12 r \frac {2\pi r} n$$
Pulling out the constants in regards to the summation and simplifying:
$$A = \lim \limits_{n \rightarrow \infty} \frac {\pi r^2} n \sum_{i=1}^{n} 1$$
Since $\sum_{i=1}^{n} 1 = n$:
$$A = \lim \limits_{n \rightarrow \infty} \frac {\pi r^2} n n = \pi r^2$$
(3) The above is probably the solution the problem wants. But we can take this one step further and convert the sum to an integral.
$$A = \lim \limits_{n \rightarrow \infty} \sum_{i=1}^{n} \frac 12 f(x_{i-1}) \frac {b-a} n = \frac 12 \int_{a}^{b}f(x)dx$$
Finally we have:
$$A = \frac 12 \int_{0}^{2\pi r}rdx = \frac 12 rx \Big|_{0}^{2\pi r} = \frac 12 r(2\pi r) - \frac 12 r(0) = \pi r^2$$