4

The book I am using for my Abstract Algebra course is Contemporary Abstract Algebra by Joseph A. Gallian.

Let $E/F$ be a Galois extension with Galois group isomorphic to $\mathbb{Z}_2\oplus\mathbb{Z}_4$. Determine the subfield lattice for $E/F$.

I was wondering if someone could guide me into the right direction on how to solve this problem.

From what I do understand, Gal$(E/F)\cong \mathbb{Z}_2\oplus\mathbb{Z}_4$. Galois Theory, in a nutshell, is used to find how many subfields are between $E$ and $F$. If $E/F$ is "nice" then there is a one-to-one correspondence between the set of subfields and the set of subgroups.

I was able to find subgroups of the direct product $\mathbb{Z}_2\oplus\mathbb{Z}_4$. I don't know if I have found all subgroups to be honest with you. I did them by hand and wasn't sure if there was a theorem to verify if I got the right number of subgroups. The list is as follows.

  • $S_0=\{(0,0)\}$, the trivial subgroup.
  • $S_1=\{(0,0),(0,2)\}$
  • $S_2=\{(0,0),(1,2)\}$
  • $S_3=\{(0,0),(1,0)\}$
  • $S_4=\{(0,0),(0,1),(0,2),(0,3)\}$
  • $S_5=\{(0,0),(1,1),(0,2),(1,3)\}$
  • $S_6=\{(0,0),(0,2),(1,0),(1,2)\}$
  • $\mathbb{Z}_2\oplus\mathbb{Z}_4=\{(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)\}$

From the information I got, we can see that $\mathbb{Z}_2\oplus\mathbb{Z}_4$ has 3 subgroups of order 4 and 3 groups of order 2. Hence we have 6 subfields between $E$ and $F$. This result in the following lattice.

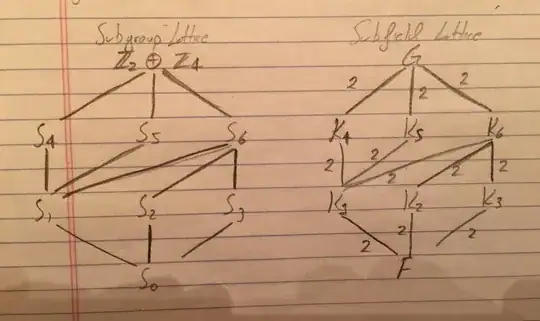
enter image description here

Am I on the right track? Would the approach be similar if the Galois group was isomorphic to $\mathbb{Z}_3\oplus\mathbb{Z}_4$? Would there be a faster way to find the subgroups of direct products?

Sorry for the rather long read. I sincerely thank you for taking the time to read this post. I greatly appreciate any assistance you may provide.

user26857
  • 52,094
Kevin_H
  • 1,731

1 Answers1

3

Seems correct, based on a cursory reading of the subgroups, I will assume you have them correct, and refer you to this question for a complete description of the subgroups of a direct product. Subgroups of a direct product

I feel that I should point out that you have written $G$ at the top of your diagram for the fields rather than $E$. Also while this is a correct drawing of the lattice by the symmetry of the lattice itself, I feel that I should make certain that you are aware that $K_1$ does not correspond to $S_1$, but rather $S_6$, and $F$ corresponds to $\mathbb{Z}_2\oplus \mathbb{Z}_4$ rather than $S_0$ as is suggested by the way the diagrams have been drawn in parallel. If this was intentional, I mean no offense, just wished to point it out in case it wasn't.

Community
  • 1
jgon
  • 28,469
  • thank you for pointing these things out. If you don't mind me asking, why does $K_1$ correspond to $S_6$? And why does $F$ correspond to $\mathbb{Z}_2\times\mathbb{Z}_4$? Small details like this still confuse me here and there. Thank you once again for your help. It helps me a lot. – Kevin_H Apr 28 '15 at 06:25
  • 1
    The subfield you get corresponds to the fixed field of the subgroup of the Galois group. So since $F$ is fixed by all the automorphisms in the Galois group, (and since the extension is Galois), the fixed field of the Galois group is $F$ and so the whole group $\mathbb{Z}_2\times\mathbb{Z}_4$ corresponds to $F$. In general small groups correspond to big fields, and vice versa. Since $K_1$ has dimension two over $F$, it corresponds to a group with index $2$ or size $4$ in the Galois group. Then since the diagram has to line up still, it must correspond to $S_6$. – jgon Apr 28 '15 at 06:31
  • 1
    The reason the index should be 2, is that the Galois group of an intermediate field extension is the quotient of the Galois group $G$ of $K/F$ by the automorphisms that fix the intermediate field $L$. – jgon Apr 28 '15 at 06:32