2

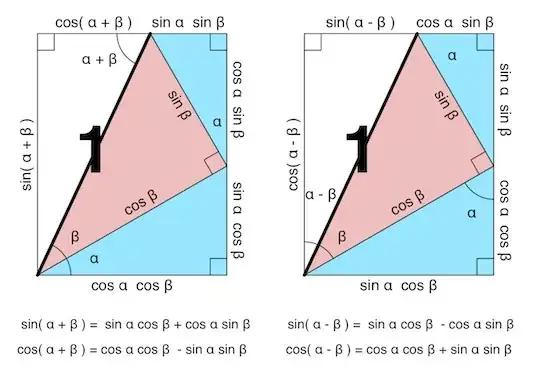
I am trying to simplify the expression $2\cos^{2}6x-1$.

The book got the answer of $\cos 12 x$ by doing $2\cos^{2}6x-1 = \cos2\left(6x\right) = \cos12x$

It said the double angle is $12x$. I don't know how $2\cos^{2}6x-1$ got to $\cos2\left(6x\right)$, can anyone explain how this works?

It said it used cosine of double-angle formula, but I am not sure how it got the answer.

user101750
  • 71
  • 6
  • Do you know what the cosine double angle formula is? It's easily available through google. – Asvin Apr 24 '15 at 03:36

4 Answers4

5

Take $$\cos2\theta=2\cos^2\theta-1$$ and substitute $\theta=6x$.

David
  • 82,662
4

$$\cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) = 2\cos^2(\theta) - 1$$ Since $\cos^2(\theta) + \sin^2(\theta) = 1$

jameselmore
  • 5,207
3

To prove the cosine double angle identities, we need the sum identity for cosine. That is, $\cos(x+y) = \cos x\cos y - \sin x \sin y.$ For a proof of this, see the picture below.

Now taking $y=x$, we get $\cos(2x) = \cos^2x - \sin^2x$. Now since $\sin^2x + \cos^2x = 1$, we have $\cos(2x) = \cos^2x - (1-\cos^2 x)$.

Simplifying, we have $\cos(2x) = 2\cos^2x - 1.$

enter image description here

Andrey Kaipov
  • 2,857
  • 1
  • 18
  • 23
0

I get:

$$2cos^2(6x)-1=cos(12x)$$

Verify the identity:

$$2*\frac{1+cos(12x)}{2}-1{=}cos(12x)$$ $$1+cos(12x)-1=cos(12x)$$ $$cos(12x)=cos(12x)$$

Now the left hand side and right hand side are identitcal!

Jan Eerland
  • 28,671