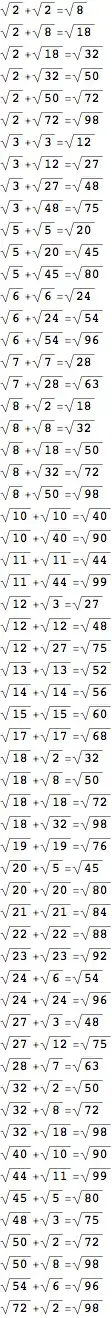26

I initially was wondering if it were possible for there to be three $x,y,z \in \mathbb{Q}$ and $\sqrt{x},\sqrt{y},\sqrt{z} \notin \mathbb{Q}$ such that $\sqrt{x} + \sqrt{y} = \sqrt{z}$. I had suspected not, but then I found $x = \dfrac{1}{2}, y = \dfrac{1}{2}$ and thus $\sqrt{x} + \sqrt{y} = \sqrt{2}$.

I suspect there are no integer solutions where the numbers are not all square, but I couldn't prove it. Nonetheless I figured I'd ask if it were possible when $x, y, z \in \mathbb{N}$ and $\sqrt{x},\sqrt{y},\sqrt{z} \notin \mathbb{N}$ that $\sqrt{x} + \sqrt{y} = \sqrt{z}$? And if not, can someone prove it?

Tyg13
  • 549
  • 7
    $\sqrt2+\sqrt8=\sqrt{18}$. That's because, reducing the roots, we have $\sqrt2+2\sqrt2=3\sqrt2$. Note that $xy=2\cdot8=16$, a square, which is guaranteed by user24142. – Akiva Weinberger Apr 24 '15 at 02:34
  • 2
    A spreadsheet would answer the question. Put $x$ in the first column, $y$ in the first row and $(\sqrt x + \sqrt y)^2$ in the array. Look by eye for integers. You will find them quickly. To fill the array, type the upper left cell, paying attention to fixed/variable coordinates with dollar signs. Copy left, copy down, done – Ross Millikan Apr 24 '15 at 04:00
  • Special case of the Lemma here. – Bill Dubuque Apr 24 '15 at 15:42

3 Answers3

46

If you square both sides, you have $x + y + 2\sqrt{xy} = z$ which can be satisfied if and only if $\sqrt{xy}$ is an integer (it can't be a half integer). So, that's the condition, if $xy$ is a square then you're fine, otherwise, its unsolvable.

user24142
  • 3,732
  • 5
    ... and in this case, with $g = \gcd(x,y)$, we have $x = u^2 g$ and $y = v^2 g$ for some coprime integers $u,v$, i.e. the equation is $\sqrt{u^2 g} + \sqrt{v^2 g} = \sqrt{(u+v)^2 g}$. – Robert Israel Apr 24 '15 at 02:38
  • So if $xy$ is a square, that implies $x=y$. I see. So we will never have any two distinct $x,y$ such that $\sqrt{x} + \sqrt{y} = \sqrt{z}$ – Tyg13 Apr 24 '15 at 02:39
  • 3
    Not at all. Consider $x = 3$ and $y = 12$, then $\sqrt{3} + \sqrt{12} = \sqrt{x} +\sqrt{y} = \sqrt{x+y + 2\sqrt{xy}} = \sqrt{27}$. – user24142 Apr 24 '15 at 02:42
  • Ah, you're right. I didn't really think about that. Rookie mistake, I guess. – Tyg13 Apr 24 '15 at 02:44
  • 3
    Don't sweat it. We're all learning something. – user24142 Apr 24 '15 at 02:46
  • More generally see the Lemma here. – Bill Dubuque Apr 24 '15 at 15:43
  • 1
    In the example $x=3,y=12$ one of the radicands, namely $y=12$, is not square-free. For that reason many people prefer to not write $\sqrt{12}$ and use $2\sqrt{3}$ instead. The relation becomes $\sqrt{3}+2\sqrt{3}=3\sqrt{3}$ which looks less fascinating. If we require that both radicands $x$ and $y$ are square-free, the only way the criterion of this answer can be satisfied is indeed $x=y$, so @Tyg13 becomes right in that sense. And $\sqrt{x}+\sqrt{x}=\sqrt{4x}=2\sqrt{x}$ is again dull. So: If you pull out all square factors so what remains under the radical signs is square-free, no surprises. – Jeppe Stig Nielsen Apr 25 '15 at 11:28
  • 3
    @JeppeStigNielsen: Yes, this is also what Robert Israel was saying. All of these can be written as $u\sqrt{g} + v\sqrt{g} = (u+v)\sqrt{g}$ and you're right, no surprises. – user24142 Apr 25 '15 at 19:30
12

Some examples for each variable $x$ and $y$ up to 100:

enter image description here

David G. Stork
  • 29,774
9

$\sqrt{x}+\sqrt{x}=2\sqrt{x}=\sqrt{4x}$. For example: $\sqrt{3}+\sqrt{3}=\sqrt{12}$.