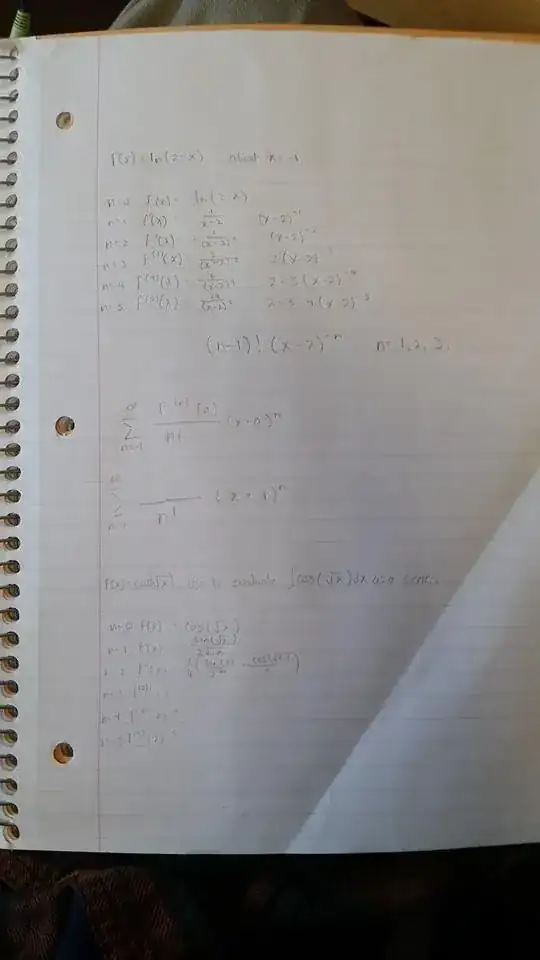Taylor series and Maclaurin series problems

Question

I'm currently working on these two problems, and I'm getting really confused with them. Can someone walk me through them?

Find the Maclaurin Series for $f(x)=\cos\left(\sqrt x\right)$ and use it to evaluate $\int\cos\left(\sqrt x\right)\mathrm dx$ as a series.

Find the Taylor Series for $f(x)=\ln(2-x)$ about $x=-1$.

Here is a tutorial to type your question with Latex. – Aaron Maroja Apr 21 '15 at 14:13 — Aaron Maroja, Apr 21 '15 at 14:13

Aaron Maroja · Answer 1 · 2015-04-21T14:23:36.623

0

Hint:

$1)$ $$\cos (x ^{1/2}) = \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n/2}}{(2n)!} = \sum_{n=0}^{\infty} (-1)^n \frac{x^{n}}{(2n)!}$$

If $[a,b] \subset (-1,1)$ then you may use termwise integration.

$2)$ $$\ln (2 - x) = \ln (3 - 1 - x) = \ln (3 - (x + 1)) = \ln 3 + \ln \Big(1 -\frac{1}{3}(x + 1) \Big)$$

edited Apr 21 '15 at 14:23

answered Apr 21 '15 at 14:09

Aaron Maroja

17,571

Was my work for the taylor series question correct up to the point I got to? – user231507 Apr 21 '15 at 14:17
Please, write in Latex, it's way better. – Aaron Maroja Apr 21 '15 at 14:24
Do you know the series of $\ln (1 - x)$? And $\cos x$? – Aaron Maroja Apr 21 '15 at 14:27
Im not sure how to use latex sorry. I do not know the series of the two. – user231507 Apr 21 '15 at 14:30
I've just linked to a tutorial to use latex. And it would be very helpful if you knew them. It's not difficult to derive them, at all. You may check here and here. – Aaron Maroja Apr 21 '15 at 14:36
You're most welcome! One more thing, I believe you should also read this thread. – Aaron Maroja Apr 21 '15 at 14:44

Taylor series and Maclaurin series problems

1 Answers1