Since I have seen this graph for only real numbers (source)
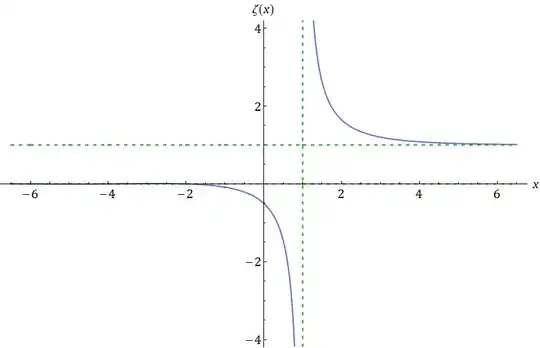 - I have start thinking about to approximate the zeta function into a more elementary function: Hyperbola:
- I have start thinking about to approximate the zeta function into a more elementary function: Hyperbola:
$\zeta(x)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^x} \rightarrow
H(x)=\frac{\alpha x+\beta}{\lambda x-x_0}+y_0$ for x>1
To fit our hyperbola we gonna need particular values of the Riemann zeta function, like:
$(2;\frac{\pi^2}{6})$ and $(4;\frac{\pi^4}{90})$
One of the variables for $H(x)$ is $x_0=1$
Of course $y_0$ should be $1$ but we gonna set $y_0=0$ and $\alpha=0$ as well.
Hense:
$h(x)=\frac{\beta}{\lambda x-1}$
(For X variables we need (at least) X points to find our formula)
Result: $h(x)=\frac{\pi^4}{6}\frac{1}{30-\pi^2+\frac{4(\pi^2-15)}{x}}$ for $1<x<5.2$
Solving for $h(x)=50$ we get $x=\frac{4(\pi^2-15)}{\pi^2(\frac{\pi^2}{300}+1)-30}\approx1.036$ not really close but by this simplification is good.
Epilog: A $H(x)$ can be fit for $x<1$ as well- here an example:
Via $(-1;-\frac{1}{12})$,$(0;-\frac{1}{2})$ and $(\frac{1}{2};\zeta(\frac{1}{2}))$ I have fit:
$h_2(x)=\frac{5(b+1)|x|}{12(b|x|+1)}-\frac{1}{2}$;where $b=\frac{17+24\zeta(\frac{1}{2})}{1+12\zeta(\frac{1}{2})}$;$x<1$
