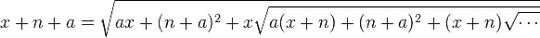How to generate complicated looking identities such as $\sqrt [3] {2 + \sqrt 5} - \sqrt [3] {2 - \sqrt 5}=1$ easily?

Question

How to generate complicated looking identities, or even more complicated looking identies such as $\sqrt [3] {2 + \sqrt 5} - \sqrt [3] {2 - \sqrt 5}=1$ easily?

I saw the identity to be shown. What is I think would be more interesting would be the origin of what ever it is that can produce even more complicated looking identities with relative ease (by relative ease I mean subbing a value and generating the identity in a mechanical fashion, no matter how laborious or long that procedure takes)

It helps that $\left(\frac{1+\sqrt{5}}{2}\right)^3 = 2 + \sqrt{5}, \left(\frac{1-\sqrt{5}}{2}\right)^3 = 2 - \sqrt{5}$. — Rolf Hoyer, Apr 19 '15 at 04:14
Here's another one: $$\sqrt{1+2\sqrt{1+3\sqrt{1+\ldots}}}=3$$ — Prasun Biswas, Apr 19 '15 at 04:15
But in general, I don't think there's any such way to "generate" complicated results. Because not every result has the same origin. — Prasun Biswas, Apr 19 '15 at 04:16
@PrasunBiswas : holy hell, what generates identities like that? — jimjim, Apr 19 '15 at 04:18
@PrasunBiswas : yes I agree nothing can be that general, is there even a taxonomy of identies or the their generating families exist? — jimjim, Apr 19 '15 at 04:19
@PrasunBiswas : that specific result or a more general form that makes that as a specific value? — jimjim, Apr 19 '15 at 04:21
Check out the answers posted by me and YoTengoUnLCD that provides somewhat of an useful answer to your question. — Prasun Biswas, Apr 19 '15 at 04:50

YoTengoUnLCD · Answer 1 · 2015-04-19T04:24:49.503

An example: $$ 1=\sqrt{2-1} \longrightarrow1=\sqrt{2-\sqrt{2-1}} $$ Repeat infinitely many times: $$ 1=\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{2...}}}} $$

You can check this is true: $$ x=\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{2...}}}} \longrightarrow x=\sqrt{2-x} $$ $$ x^2=2-x \longrightarrow x_1=1 $$ $x_2=-2$ can be discarded as we're taking a square root.

It's worth to note that what Prasun Biswas and I have posted here are expressions called "nested radicals".

Ramanujan was a mathematician that greatly raised interest and got some great conclusions about them at his time.

http://en.wikipedia.org/wiki/Nested_radical is worth a look.

score 1 · Accepted Answer · edited Mar 09 '17 at 17:32

1

Here's a nice "generator" of the result I commented in the comments.

edited Mar 09 '17 at 17:32

Community

1

answered Apr 19 '15 at 04:20

Prasun Biswas

6,334

Plugging $x=2,n=1,a=0$ gives us the specific result of the problem that Ramanujan posed. – Prasun Biswas Apr 19 '15 at 04:29

How to generate complicated looking identities such as $\sqrt [3] {2 + \sqrt 5} - \sqrt [3] {2 - \sqrt 5}=1$ easily?

2 Answers2