Why does the graph of $y=\gcd \left(\frac{x}{y},xy\right)$ seem to have 4 "straight" lines?
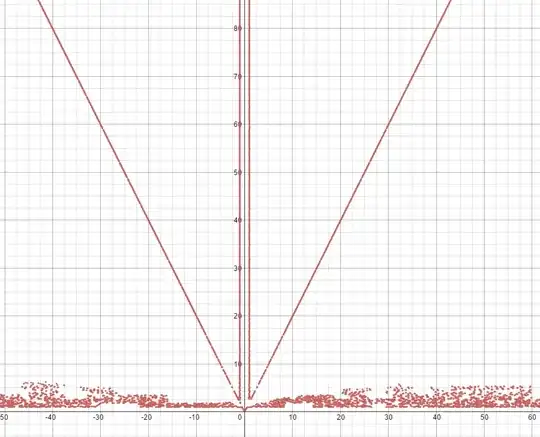
Using https://www.desmos.com/calculator for plotting.
Asked
Active
Viewed 303 times
2
-
1I don't quite understand your graph, what exactly are the two axes? – Gregory Grant Apr 17 '15 at 21:05
-
I honestly cannot figure out, what that applet does! Except that typing in constant $a,b$ in $\gcd(a,b)$, it seems to act as $\gcd(\operatorname{round}(a),\operatorname{round}(b))$. – String Apr 17 '15 at 21:34
-
I've been trying to figure it out myself, @String. I've assumed it's the 'classic' gcd, i.e, the one here so that $\gcd\left(\frac{a}{b},\frac{c}{d}\right) = \frac{1}{bd}\gcd(ad, bc)$, but the 'lines' corresponding to $x = \pm 1$ aren't really lines; they're zig-zags. Even so, it's quite hard to find any rational points that satisfy the equation... we definitely have 'pseudo lines' of $x = \pm 1$ and $y = \pm 2x$, but I can't figure them out. – pjs36 Apr 17 '15 at 21:47
1 Answers
0
This is due to some bad software and/or asking software to do something it wasn't meant to do.
Suppose $y=\gcd(x/y,xy)$. Then $y$ must divide $x$, else $x/y$ is not an integer, and the gcd would not be defined.
Say $x=yk$ for some integer $k$.
Then $x/y$ = $k$, and $\gcd(x/y,xy)=\gcd(k,y^2 k) = k$.
So $k=y$, i.e., $x=y^2$.
In fact, $y=\gcd(x/y,xy)$ if and only if $x=y^2$.
So, for example, you should see the points $(1,1)$, $(4,2)$, $(9,3)$, etc., in the plot. That's all that should be there.
However, the software is not smart enough to conclude this, so it does some kind of shotgun approach on your implicit equation, and as String commented, there must be some rounding in order for it to make sense of $x/y$ when it is not an integer. Then it tries to "connect the dots". The result is it gives you lots of points that are not solutions (i.e., nonsense), while leaving out the points that are solutions (since there are no nearby solutions, and it can't check everywhere).
Matthew Conroy
- 11,234