6

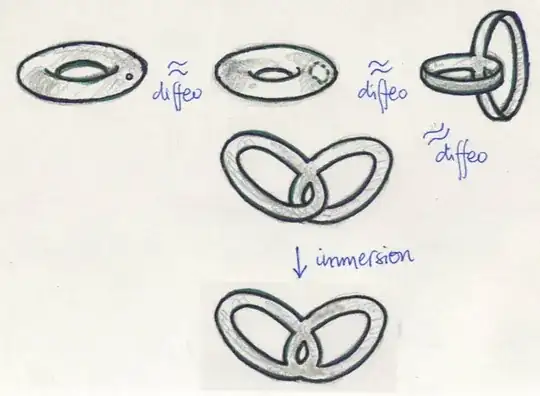
Let $S^1 \times S^1$ be the $2$-torus. If a point $a=(p,q)$ of the torus is removed, i.e., it is punctured at one point then how can I show that it can be immersed in the plane, i.e., in $\Bbb{R}^2$?

I have the idea of decomposing the punctured torus into two intersecting cylinders and then immersing each of them to $\Bbb{R}^2$, but the problem is by this way even if we make that the intersecting region mapped to same region, we cannot define an immersion on the whole the two immersions may not agree pointwise on the intersection. I have got stuck here.

Thanks in advance for any kind of help.

tandra
  • 309

1 Answers1

14

What follows is a topologist's solution, but I believe quite revealing.immersion

A torus minus one point is a torus minus a disc. Expanding the disc one gets two cilinders (without border, but for the picture it's easier to draw it) attached as seen. These are just a couple of annuli with a common rectangle, which can be projected onto the plane. It's an open inmersion, of course not injective.

Community
  • 1
Jesus RS
  • 4,189
  • 2
    How an explicit expression for immersion can be given..i.e a general argument that will prove that the n-torus\a-point can also be immersed in R^n? – tandra Apr 16 '15 at 14:37
  • @tandra b) Follows from exercise 4 (next exercise): Consider the product of $n$ circles (''$1$-spheres'') and remove a point $p$. Once you have immersed $S^1\times S^1{p}$ in $\mathbb R^2$, what you get is a product of $n-2$ $1$-spheres times $R^2$. According to the answer provided here that embeds into $\mathbb R^{n-2+1}\times \mathbb R^= \mathbb R^n$. – Dog_69 Oct 24 '19 at 15:43
  • 1
    I think there's trouble with factors: $S^1\times S^1\times S^1\setminus{(a,b,c)}$ and $S^1\times\big(S^1\times S^1\setminus{(b,c)}\big)$. – Jesus RS Oct 25 '19 at 16:42
  • @JesusRS Yes, it seems so. Thank you. Do you have a solution? – Dog_69 Oct 28 '19 at 11:41