The question is to give a formula in $x$ and $y$ that gives all three sides of an equilateral triangle. The formula should not be true for points that are not part of the perimeter of the triangle. By this sub-problem, I am trying to understand deeper the page 809 and attack problem 11 on page 813 here -- there the purpose of parametrization is to find solutions to the partial differentials $\triangle u=0$, so-called boundary-problem and Dirichet's condition.
Trial 0
J.M. hinted the parametrization here, through $(1,0)$?
$$\displaystyle r=\frac{\cos\left(\frac{\pi}{n}\right)}{\cos\left(\left(\theta \mod \frac{2\pi}{n}\right) -\frac{\pi}{n}\right)} \;$$

I cannot understand the order of the division yet. I can understand the radius part but not why a line in the triangle, it must be due to some identity. Look I could do this with a small change (reciprocal of the radius):
n=3;
theta=(0:999)/1000;
r=cos(2*pi*(n*theta)%%1/n-pi/n)/cos(pi/n);
plot(r*cos(2*pi*theta),r*sin(2*pi*theta),asp=1,xlab="X",ylab="Y",
main=paste("Regular ",n,"-gon",sep=""),type='l');
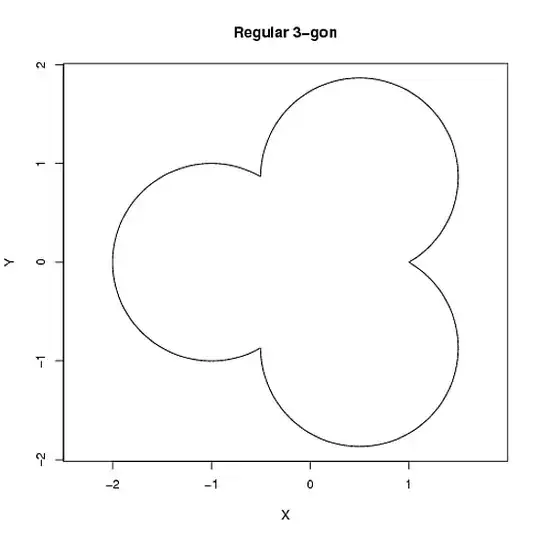
n=3;
theta=(0:999)/1000;
#r=cos(pi/n)/cos(2*pi*(n*theta)%%1/n-pi/n);
r=cos(2*pi*(n*theta)%%1/n-pi/n)/cos(pi/n);
plot(r*cos(2*pi*theta),r*sin(2*pi*theta),asp=1,xlab="X",ylab="Y",
main=paste("Regular ",n,"-gon",sep=""),type='l');
r=cos(pi/n)/cos(2*pi*(n*theta)%%1/n-pi/n);
lines(r*cos(2*pi*theta),r*sin(2*pi*theta),asp=1,xlab="X",ylab="Y",
main=paste("Regular ",n,"-gon",sep=""),type='l');
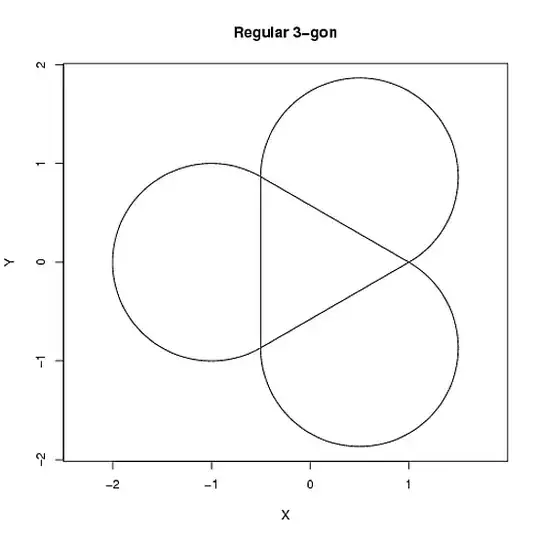
Trial 1
David Wallace instructed me here to use polar coordinates and the floor function to describe the perimeter of the triangle apparently so that
$$\begin{cases}x=r\cos(\theta)\\y=r\sin(\theta)\end{cases}$$
$$r\cos\left(\frac{2\pi}{3}\left(\frac{3\theta}{2\pi}-\left\lfloor\frac{3\theta}{2\pi}\right\rfloor\right) -\frac{\pi}{3}\right) = 1$$
...cannot understand this at all, hard to see the parametric form here.
Perhaps related
Something about plotting the function here