I've dealt with this some monthes ago and have this in some scribbles. Don't know whether this is of any help.
From the ansatz (where m is the horizontal,vertical and diagonal sum):
$$ \begin{array} {rrr|r} & & & m \\
a^2 & b^2 & c^2 & m \\
d^2 & e^2 & f^2 & m \\
g^2 & h^2 & i^2 & m \\
\hline
m&m&m&m
\end{array} $$
writing this as an array of equations and using Gauss-reduction I arrived at the following magic square with three free parameters $[e,i,h]$ :
$$ \begin{array} {rrr|r} & & & 3e^2 \\
2e^2-i^2 & 2e^2 -h^2& -e^2 +h^2 + i^2 & 3e^2 \\
-2e^2+h^2+2i^2 & e^2 & 4e^2-h^2-2i^2 & 3e^2 \\
3e^2-h^2-i^2 & h^2 & i^2 & 3e^2 \\
\hline
3e^2&3e^2&3e^2&3e^2
\end{array} $$
If I recall correctly I've seen, that the parameters must be odd and not divisible by $3$ or in other words $e^2,i^2,h^2$ must be congruent $1$ modulo $24$.
I didn't proceed then, however perhaps that representation is of some interest for you.
[update2] Here is one more information which I forgot to include earlier. We can express the conditions on the entries in the magic square, which should also be squares, depending on the three parameters $[e,h,i]$ as a small matrix-multiplication:
$$ \begin{array} {r}
&&&&|&e^2| \\
&&&&|&h^2| \\
&&&&*|&i^2| \\
\hline
|& 2 & 0 & -1| & |&a^2| \\
|& 2 & -1 & 0| & |&b^2| \\
|&-1 & 1 & 1| & = |&c^2| \\
|&-2 & 1 & 2| & |&d^2| \\
|& 4 & -1 &-2| & |&f^2| \\
|& 3 & -1 &-1| & |&g^2| \\
\end{array} $$
I found it much tempting to try to make something out of that structural description to say something about the possibilities for all entries simultanously to be squares, but have not yet a better expression.
[update 1] The comments below motivated me to simply try out that parametrized problem. Using a Pari/GP-routine with a three-fold loop for the base-parameters $[e,h,i]$ I got this $7$-squares-solutions in 53 secs (which is also the given $7$-squares solution shown in the thread's initial question):
$$ \small \begin{bmatrix}
205^2 & 527^2 & 222121 \\
360721 & 425^2 & 23^2 \\
373^2 & 289^2& 565^2
\end{bmatrix}
\small
\begin{bmatrix}
222121 & 527^2 & 205^2 \\
23^2 & 425^2 & 360721 \\
565^2 & 289^2 & 373^2
\end{bmatrix} $$
The symmetry of the two solutions indicate, that I could have halved the consumption of time If I had some smarter search-criteria.
With some improved criteria for the loop (100 sec, $e$ used up to 3000) I found some more solutions - unfortunately the're only the trivial multiples of the first one... :
$$ \small \begin{matrix}
& a^2 & b^2 & c^2 & d^2 & e^2 & f^2 & g^2 & h2 & i^2 \\
\hline
& 410^2 & 1054^2 & 2^2\cdot 151 \cdot 1471 & 2^2\cdot 137 \cdot 2633
& 850^2 & 46^2 & 746^2 & 578^2 & 1130^2 \\
& 615^2 & 1581^2 & 3^2\cdot 151 \cdot 1471 & 3^2\cdot 137 \cdot 2633
& 1275^2 & 69^2 & 1119^2 & 867^2 & 1695^2 \\
& 820^2 & 2108^2 & 4^2\cdot 151 \cdot 1471 & 4^2\cdot 137 \cdot 2633
& 1700^2 & 92^2 & 1492^2 & 1156^2 & 2260^2 \\
& 1025^2 & 2635^2 & 5^2\cdot 151 \cdot 1471 & 5^2\cdot 137 \cdot 2633
& 2125^2 & 115^2 & 1865^2 & 1445^2 & 2825^2 \\
& 1230^2 & 3162^2 & 6^2\cdot 151 \cdot 1471 & 6^2\cdot 137 \cdot 2633
& 2550^2 & 138^2 & 2238^2 & 1734^2 & 3390^2 \\
& \vdots \\
k^2*\ldots&205^2 & 527^2 & 151 \cdot 1471 & 137 \cdot 2633 & 425^2& 23^2 & 373^2 & 289^2 & 565^2\\
& \vdots \end{matrix}
$$
Obviously there is no number $k^2$ which would make the entries in columns $c^2$ and $d^2$ a perfect square, so this scheme cannot provide a better solution for higher $k$.
Here is the Pari/GP-code (updated)
isin(x,vgl)=if (x<1,return(1)); for(k=1,#vgl,if(x==vgl[k],return(1)));return(0);
{ listsqsq(max_e=100,max_nosq=3,min_e=1)= local(a,b,c,d ,f,g, no_sq,a2,b2,c2,d2,e2,f2,g2,h2,i2,list,li);
list=vectorv(20000);li=0;
for(e=min_e,max_e, e2=e^2;
for(h=1,ceil(1.5e), if(h==e,next()); \ no higher h needed
h2=h^2;
b2=2e2 - h2; if(isin(b2,[e2,h2]), next());
if(issquare(b2)==0, next());
b=sqrtint(b2);
for(i=sqrtint(e2-ceil(h2/2)),sqrtint(2*e2-floor(h2/2))+1, if(isin(i,[e,h,b]),next()); \\ no higher i needed
i2=i^2;no_sq=0;
g2= b2 +e2-i2; if (isin(g2,[b2,e2,h2,i2]) ,next()); if(issquare(g2)==0,next()); g=sqrtint(g2);
a2= 2*e2 -i2; if (isin(a2,[b2,e2,h2,i2,g2]) ,next()); if(issquare(a2)==0,a=-a2;no_sq++, a=sqrtint(a2));
c2=-e2+h2+i2; if (isin(c2,[b2,e2,h2,i2,g2,a2]) ,next()); if(issquare(c2)==0,c=-c2;no_sq++, c=sqrtint(c2));
d2=-2*e2+h2+2*i2; if (isin(d2,[b2,e2,h2,i2,g2,a2,c2]) ,next()); if(issquare(d2)==0,d=-d2;no_sq++, d=sqrtint(d2));
f2= 4*e2-h2-2*i2; if (isin(f2,[b2,e2,h2,i2,g2,a2,c2,d2]),next()); if(issquare(f2)==0,f=-f2;no_sq++, f=sqrtint(f2));
if(no_sq>max_nosq,next());
idx=prime(e)*prime(h)*prime(i)*prime(g);
li++;list[li]=[a,b,c,d,e,f,g,h,i,log(idx),no_sq];
)
);
);
if(li==0 , return(Mat([0])));
list=Mat(list[1..li]);
list=vecsort(list~,[10,4,7,8,3,6,7])~;
return(list);}
[update 3] An account of the possible 13 primitive solutions (no rotations, no reflections) on behalf of a comment of @andrewpalfreyman; this is an independent validation of A. Bremner's list:
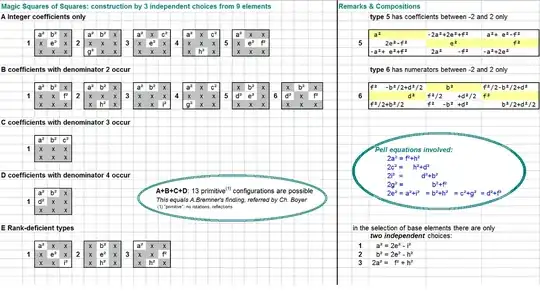
I generated this list by computing all initial solutions and identifying the occuring coefficients. Duplicate sets of coefficients were ignored, and only $13$ distinct sets of coefficients remained. With this, the according $3 \times 3$-configurations are documented with their first occurences.
Interestingly we have sets of coefficients having only integer values, or half integer etc; my own $7$-squares solutions is here a rotation of configurations A1.
Moreover,three primitive rank-deficite initial configurations were as well identified, and I explain the reason for the rank-deficience.
